Question

13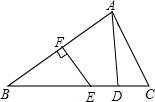．如图，在△ABC中，AB的垂直平分线EF交BC于点E，交AB于点F，D为线段CE的中点，∠CAD=20°，∠ACB的补角是110°．求证：BE=AC．

Answer 1

分析 首先证明AD是线段EC的垂直平分线，根据垂直平分线的性质即可证明．

解答 证明：连接AE，
∵∠ACB的外角是110°，
∴∠ACB=180°-110°=70°，
∵∠DAC=20°，
∴∠DAC+∠ACD=90°，
∴AD⊥EC，
∵DE=DC，
∴AE=AC，
∵EF垂直平分AB，
∴EA=EB，
∴BE=AC．

点评 本题考查三角形外角的定义、线段垂直平分线的性质、垂直的定义，熟练掌握垂直平分线的性质是解决问题的关键．