题目内容
6.如图①,在矩形纸片ABCD中,AB=$\sqrt{3}$+1,AD=$\sqrt{3}$.(1)如图②,将矩形纸片向上方翻折,使点D恰好落在AB边上的D′处,压平折痕交CD于点E,则折痕AE的长为$\sqrt{6}$.
(2)如图③,再将四边形BCED′沿D′E向左翻折,压平后得四边形B′C′ED′,B′C′交AE于点F,则四边形B′FED′的面积为$\sqrt{3}$-$\frac{1}{2}$.
(3)如图④,将图②中的△AED′绕点E顺时针旋转α角,得△A′ED″,使得EA′恰好经过顶点B,求弧D′D″的长$\frac{5\sqrt{3}π}{12}$.(结果保留π)
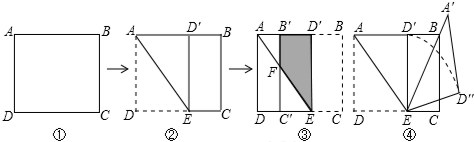
分析 (1)先根据图形反折变换的性质得出AD′,D′E的长,再根据勾股定理求出AE的长即可;
(2)由(1)知,AD′=$\sqrt{3}$,故可得出BD′的长,根据图形反折变换的性质可得出B′D′的长,再由等腰直角三角形的性质得出B′F的长,根据梯形的面积公式即可得出结论;
(3)先根据直角三角形的性质求出∠BEC的度数,由翻折变换的性质可得出∠DEA的度数,故可得出∠AEA′=75°=∠D′ED″,由弧长公式即可得出结论.
解答 解:(1)∵△ADE反折后与△AD′E重合,
∴AD′=AD=D′E=DE=$\sqrt{3}$,
∴AE=$\sqrt{AD{′}^{2}+D′{E}^{2}}$=$\sqrt{(\sqrt{3})^{2}+(\sqrt{3})^{2}}$=$\sqrt{6}$;
(2)∵由(1)知AD′=$\sqrt{3}$,
∴BD′=1,
∵将四边形BCED′沿D′E向左翻折,压平后得四边形B′C′ED′,
∴B′D′=BD′=1,
∵由(1)知AD′=AD=D′E=DE=$\sqrt{3}$,
∴四边形ADED′是正方形,
∴B′F=AB′=$\sqrt{3}$-1,
∴S梯形B′FED′=$\frac{1}{2}$(B′F+D′E)•B′D′=$\frac{1}{2}$($\sqrt{3}$-1+$\sqrt{3}$)×1=$\sqrt{3}$-$\frac{1}{2}$;
故答案为:(1)$\sqrt{6}$;(2)$\sqrt{3}$-$\frac{1}{2}$;
(3)∵∠C=90°,BC=$\sqrt{3}$,EC=1,
∴tan∠BEC=$\frac{BC}{CE}$=$\sqrt{3}$,
∴∠BEC=60°,
由翻折可知:∠DEA=45°,
∴∠AEA′=75°=∠D′ED″,
∴$\widehat{D′D″}$=$\frac{75π•\sqrt{3}}{180}$=$\frac{5\sqrt{3}π}{12}$.
点评 本题考查的是图形的翻折变换,熟知图形翻折不变性的性质是解答此题的关键.

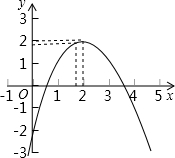 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:①abc>0;②9a+4b+c<0;③9a-c+1>0;④a<-$\frac{1}{8}$,其中,正确的结论的个数是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:①abc>0;②9a+4b+c<0;③9a-c+1>0;④a<-$\frac{1}{8}$,其中,正确的结论的个数是( )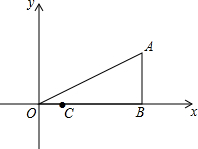 如图,在平面直角坐标系中,△ABO为直角三角形,∠ABO=90°,∠AOB=30°,AB=$\sqrt{3}$.
如图,在平面直角坐标系中,△ABO为直角三角形,∠ABO=90°,∠AOB=30°,AB=$\sqrt{3}$.
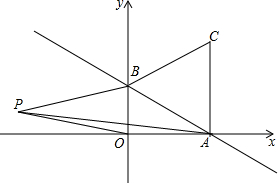 如图,一次函数y=-$\frac{\sqrt{3}}{3}$x+1的图象与x轴、y轴分别交于点A、B,以线段AB为边在第一象限内作等边△ABC,
如图,一次函数y=-$\frac{\sqrt{3}}{3}$x+1的图象与x轴、y轴分别交于点A、B,以线段AB为边在第一象限内作等边△ABC,