题目内容
9. 二次函数y=ax2+bx的图象如图,若一元二次方程ax2+bx+m=0有实数根,求m的取值范围.
二次函数y=ax2+bx的图象如图,若一元二次方程ax2+bx+m=0有实数根,求m的取值范围.
分析 结合图象可得y≥-3,即ax2+bx≥-3,由ax2+bx+m=0可得ax2+bx=-m,则有-m≥-3,即可解决问题.
解答 解:
由图可知:y≥-3,即ax2+bx≥-3,
∵ax2+bx+m=0,
∴ax2+bx=-m,
∴-m≥-3,
∴m≤3.
点评 本题主要考查抛物线与一元二次方程之间的关系、解一元一次不等式等知识,利用数形结合的思想是解决本题的关键.

练习册系列答案
相关题目
1. 如图,点E在BC上,点A、E、D在同一条直线上,AB⊥BC,CD⊥BC,若测得BE=20m,EC=10m,CD=20m,则河宽AB=( )
如图,点E在BC上,点A、E、D在同一条直线上,AB⊥BC,CD⊥BC,若测得BE=20m,EC=10m,CD=20m,则河宽AB=( )
 如图,点E在BC上,点A、E、D在同一条直线上,AB⊥BC,CD⊥BC,若测得BE=20m,EC=10m,CD=20m,则河宽AB=( )
如图,点E在BC上,点A、E、D在同一条直线上,AB⊥BC,CD⊥BC,若测得BE=20m,EC=10m,CD=20m,则河宽AB=( )| A. | 60m | B. | 40m | C. | 30m | D. | 20m |
18.下列运算正确的是( )
| A. | $\sqrt{18}$$-\sqrt{2}$=2 | B. | $\sqrt{14}$×$\sqrt{2}$=2$\sqrt{7}$ | C. | ($\sqrt{3}+2)$2=7 | D. | (-2ab2)3=-6a3b6 |
19.已知四边形ABCD是平行四边形,下列结论中不正确的是( )
| A. | 当AB=BC时,它是菱形 | B. | 当AC⊥BD时,它是菱形 | ||
| C. | 当∠ABC=90°时,它是矩形 | D. | 当AC=BD时,它是正方形 |
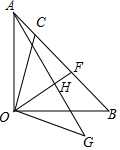 如图,△AOB为等腰直角三角形,∠AOB=90°,C是线段AB上一点,连接OC,作OG⊥OC,且OC=OG,连接AG,取CF=FB,连OF交AG于H,求证:OH⊥AG.
如图,△AOB为等腰直角三角形,∠AOB=90°,C是线段AB上一点,连接OC,作OG⊥OC,且OC=OG,连接AG,取CF=FB,连OF交AG于H,求证:OH⊥AG.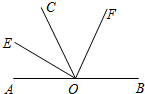 如图,O为直线AB上一点,作射线OC,OE平分∠AOC,OF平分∠BOC.
如图,O为直线AB上一点,作射线OC,OE平分∠AOC,OF平分∠BOC.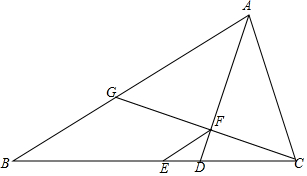 如图,AD是△ABC的平分线,E为BC的中点,EF∥AB交AD于点F,CF的延长线交AB于点G,求证:AG=AC.
如图,AD是△ABC的平分线,E为BC的中点,EF∥AB交AD于点F,CF的延长线交AB于点G,求证:AG=AC.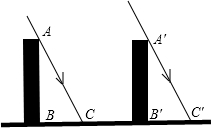 如图,太阳光线AC与A′C′是平行的,同一时刻垂直于地面的两根木杆在太阳光照射下的影子一样长,那么这辆跟木杆高度相同吗?
如图,太阳光线AC与A′C′是平行的,同一时刻垂直于地面的两根木杆在太阳光照射下的影子一样长,那么这辆跟木杆高度相同吗?