题目内容
4.|2-$\sqrt{6}}$|-$\sqrt{{{(3-\sqrt{6})}^2}}$+$\sqrt{81}$+$\root{3}{-27}$+$\sqrt{(-\frac{2}{3}}{)^2}$.分析 首先计算开方,然后从左向右依次计算,求出算式的值是多少即可.
解答 解:|2-$\sqrt{6}}$|-$\sqrt{{{(3-\sqrt{6})}^2}}$+$\sqrt{81}$+$\root{3}{-27}$+$\sqrt{(-\frac{2}{3}}{)^2}$
=$\sqrt{6}$-2-(3-$\sqrt{6}$)+9+(-3)+$\frac{2}{3}$
=$\sqrt{6}$-2-3+$\sqrt{6}$+6+$\frac{2}{3}$
=2$\sqrt{6}$+1$\frac{2}{3}$
点评 此题主要考查了实数的运算,要熟练掌握,解答此题的关键是要明确:在进行实数运算时,和有理数运算一样,要从高级到低级,即先算乘方、开方,再算乘除,最后算加减,有括号的要先算括号里面的,同级运算要按照从左到右的顺序进行.另外,有理数的运算律在实数范围内仍然适用.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
9.在△ABC中,若a=$\sqrt{2n}$,b=$\sqrt{{n}^{2}+1}$,c=n-1,则△ABC的形状是( )
| A. | 锐角三角形 | B. | 钝角三角形 | C. | 等腰三角形 | D. | 直角三角形 |
 如图,∠α和∠β的度数满足方程组$\left\{\begin{array}{l}{2∠α+∠β=235°}\\{∠β-∠α=70°}\end{array}\right.$,且CD∥EF,AC⊥AE.
如图,∠α和∠β的度数满足方程组$\left\{\begin{array}{l}{2∠α+∠β=235°}\\{∠β-∠α=70°}\end{array}\right.$,且CD∥EF,AC⊥AE. 如图,在平面直角坐标系中,直线y=-3x+3与x轴、y轴分别交于A、B两点,以AB为边在第一象限作正方形,点D恰好在双曲线上$y=\frac{k}{x}$,则k值为4.
如图,在平面直角坐标系中,直线y=-3x+3与x轴、y轴分别交于A、B两点,以AB为边在第一象限作正方形,点D恰好在双曲线上$y=\frac{k}{x}$,则k值为4.
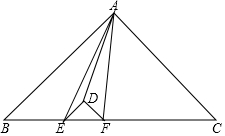 如图,等腰直角三角形DEF的斜边在等腰直角三角形ABC的斜边上,连接AE、AD、AF,于是整个图形被分成五块小三角形.其中三块的面积为S△DEF=1、S△ADE=2、S△ADF=3,那么△ABC的面积是36.
如图,等腰直角三角形DEF的斜边在等腰直角三角形ABC的斜边上,连接AE、AD、AF,于是整个图形被分成五块小三角形.其中三块的面积为S△DEF=1、S△ADE=2、S△ADF=3,那么△ABC的面积是36.