题目内容
18.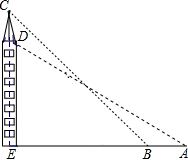 如图,在一个20米高的楼顶上有一信号塔DC,某同学为了测量信号塔的高度,在地面的A处测得信号塔下端D的仰角为30°,然后他正对塔的方向前进了8米到达地面的B处,又测得信号塔顶端C的仰角为45°,CD⊥AB于点E,E、B、A在一条直线上.信号塔CD的高度为( )
如图,在一个20米高的楼顶上有一信号塔DC,某同学为了测量信号塔的高度,在地面的A处测得信号塔下端D的仰角为30°,然后他正对塔的方向前进了8米到达地面的B处,又测得信号塔顶端C的仰角为45°,CD⊥AB于点E,E、B、A在一条直线上.信号塔CD的高度为( )| A. | 20$\sqrt{3}$ | B. | 20$\sqrt{3}$-8 | C. | 20$\sqrt{3}$-28 | D. | 20$\sqrt{3}$-20 |
分析 利用30°的正切值即可求得AE长,进而可求得CE长.CE减去DE长即为信号塔CD的高度.
解答 解:根据题意得:AB=8米,DE=20米,∠A=30°,∠EBC=45°,
在Rt△ADE中,AE=$\sqrt{3}$DE=20$\sqrt{3}$米,
∴BE=AE-AB=20$\sqrt{3}$-8(米),
在Rt△BCE中,CE=BE•tan45°=(20$\sqrt{3}$-8)×1=20$\sqrt{3}$-8(米),
∴CD=CE-DE=20$\sqrt{3}$-8-20=20$\sqrt{3}$-28(米);
故选:C.
点评 本题考查了解直角三角形-仰角俯角问题,要求学生能借助仰角构造直角三角形并解直角三角形;难点是充分找到并运用题中相等的线段.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.在一个不透明的口袋中装有5个质地、大小、颜色完全相同的小球,把它们分别标号为1,2,3,4,5,从中随机摸出一个小球,其标号不大于3的概率为( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
7.把分式方程$\frac{1}{x-3}+\frac{1-x}{3-x}=1$的两边同时乘以(x-3),约去分母,得( )
| A. | 1+(1-x)=1 | B. | 1-(1-x)=1 | C. | 1+(1-x)=x-3 | D. | 1-(1-x)=x-3 |
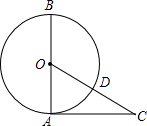 如图,AB是⊙O的直径,AC是⊙O的切线,OC交⊙O于点D,若∠C=40°,OA=9,则$\widehat{BD}$的长为$\frac{13}{2}$π.(结果保留π)
如图,AB是⊙O的直径,AC是⊙O的切线,OC交⊙O于点D,若∠C=40°,OA=9,则$\widehat{BD}$的长为$\frac{13}{2}$π.(结果保留π)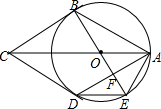 如图,AB,AD是⊙O的弦,AO平分∠BAD.过点B作⊙O的切线交AO的延长线于点C,连接CD,BO.延长BO交⊙O于点E,交AD于点F,连接AE,DE.
如图,AB,AD是⊙O的弦,AO平分∠BAD.过点B作⊙O的切线交AO的延长线于点C,连接CD,BO.延长BO交⊙O于点E,交AD于点F,连接AE,DE.