题目内容
10.在一个不透明的口袋中装有5个质地、大小、颜色完全相同的小球,把它们分别标号为1,2,3,4,5,从中随机摸出一个小球,其标号不大于3的概率为( )| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
分析 根据随机事件概率大小的求法,找准两点:①符合条件的情况数目,②全部情况的总数,二者的比值就是其发生的概率的大小.
解答 解:根据题意可得:标号不大于3有1,2,3三个球,共5个球,
从中随机摸出一个小球,其标号不大于3的概率为是$\frac{3}{5}$.
故选C.
点评 本题考查概率的求法与运用,一般方法:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=$\frac{m}{n}$,难度适中.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.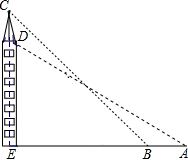 如图,在一个20米高的楼顶上有一信号塔DC,某同学为了测量信号塔的高度,在地面的A处测得信号塔下端D的仰角为30°,然后他正对塔的方向前进了8米到达地面的B处,又测得信号塔顶端C的仰角为45°,CD⊥AB于点E,E、B、A在一条直线上.信号塔CD的高度为( )
如图,在一个20米高的楼顶上有一信号塔DC,某同学为了测量信号塔的高度,在地面的A处测得信号塔下端D的仰角为30°,然后他正对塔的方向前进了8米到达地面的B处,又测得信号塔顶端C的仰角为45°,CD⊥AB于点E,E、B、A在一条直线上.信号塔CD的高度为( )
 如图,在一个20米高的楼顶上有一信号塔DC,某同学为了测量信号塔的高度,在地面的A处测得信号塔下端D的仰角为30°,然后他正对塔的方向前进了8米到达地面的B处,又测得信号塔顶端C的仰角为45°,CD⊥AB于点E,E、B、A在一条直线上.信号塔CD的高度为( )
如图,在一个20米高的楼顶上有一信号塔DC,某同学为了测量信号塔的高度,在地面的A处测得信号塔下端D的仰角为30°,然后他正对塔的方向前进了8米到达地面的B处,又测得信号塔顶端C的仰角为45°,CD⊥AB于点E,E、B、A在一条直线上.信号塔CD的高度为( )| A. | 20$\sqrt{3}$ | B. | 20$\sqrt{3}$-8 | C. | 20$\sqrt{3}$-28 | D. | 20$\sqrt{3}$-20 |
2.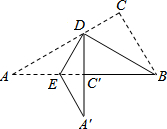 如图的实线部分是由Rt△ABC经过两次折叠得到的,首先将Rt△ABC沿BD折叠,使点C落在斜边上的点C′处,再沿DE折叠使点A落在DC′延长线上的点A′处,若图中,∠A=30°,BC=5cm,则折痕DE的长为( )
如图的实线部分是由Rt△ABC经过两次折叠得到的,首先将Rt△ABC沿BD折叠,使点C落在斜边上的点C′处,再沿DE折叠使点A落在DC′延长线上的点A′处,若图中,∠A=30°,BC=5cm,则折痕DE的长为( )
 如图的实线部分是由Rt△ABC经过两次折叠得到的,首先将Rt△ABC沿BD折叠,使点C落在斜边上的点C′处,再沿DE折叠使点A落在DC′延长线上的点A′处,若图中,∠A=30°,BC=5cm,则折痕DE的长为( )
如图的实线部分是由Rt△ABC经过两次折叠得到的,首先将Rt△ABC沿BD折叠,使点C落在斜边上的点C′处,再沿DE折叠使点A落在DC′延长线上的点A′处,若图中,∠A=30°,BC=5cm,则折痕DE的长为( )| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 2$\sqrt{5}$ | D. | $\frac{10}{3}$ |
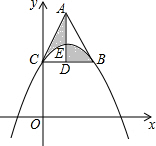 如图,在平面直角坐标系中,点C是抛物线y=a(x-3)2+k与y轴的交点,点B是这条抛物线上另一点,且BC∥x轴,以CB为边向上作等边三角形ABC,BC边上的高AD交抛物线于点E,则阴影部分图形的面积为$\frac{9}{2}$$\sqrt{3}$.
如图,在平面直角坐标系中,点C是抛物线y=a(x-3)2+k与y轴的交点,点B是这条抛物线上另一点,且BC∥x轴,以CB为边向上作等边三角形ABC,BC边上的高AD交抛物线于点E,则阴影部分图形的面积为$\frac{9}{2}$$\sqrt{3}$.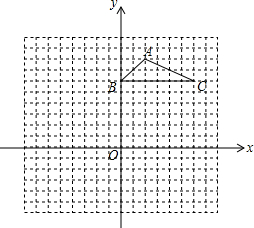 如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,△ABC的顶点都在格点上,建立如图所示的平面直角坐标系.
如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,△ABC的顶点都在格点上,建立如图所示的平面直角坐标系.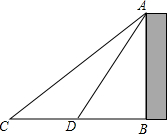 天津北宁公园内的致远塔,塔高九层,塔内四周墙壁上镶钳着历史题材为内容的瓷板油彩画或青石刻浮雕,叠双向盘旋楼梯或电梯可达九层,津门美景尽收眼底,是我国目前最高的宝塔.某校数学情趣小组实地测量了致远塔的高度AB,如图,在C处测得塔尖A的仰角为45°,再沿CB方向前进31.45m到达D处,测得塔尖A的仰角为60°,求塔高AB(精确到0.1m,$\sqrt{3}$≈1.732)
天津北宁公园内的致远塔,塔高九层,塔内四周墙壁上镶钳着历史题材为内容的瓷板油彩画或青石刻浮雕,叠双向盘旋楼梯或电梯可达九层,津门美景尽收眼底,是我国目前最高的宝塔.某校数学情趣小组实地测量了致远塔的高度AB,如图,在C处测得塔尖A的仰角为45°,再沿CB方向前进31.45m到达D处,测得塔尖A的仰角为60°,求塔高AB(精确到0.1m,$\sqrt{3}$≈1.732)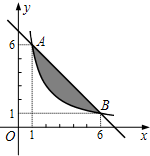 如果一个点的横、纵坐标均为整数,那么我们称这个点是格点,如图,A、B两点在函数y=$\frac{k}{x}$(x>0)的图象上,则图中阴影部分(不包括边界)所含格点的个数为3个.
如果一个点的横、纵坐标均为整数,那么我们称这个点是格点,如图,A、B两点在函数y=$\frac{k}{x}$(x>0)的图象上,则图中阴影部分(不包括边界)所含格点的个数为3个.