题目内容
13.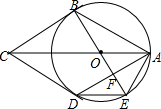 如图,AB,AD是⊙O的弦,AO平分∠BAD.过点B作⊙O的切线交AO的延长线于点C,连接CD,BO.延长BO交⊙O于点E,交AD于点F,连接AE,DE.
如图,AB,AD是⊙O的弦,AO平分∠BAD.过点B作⊙O的切线交AO的延长线于点C,连接CD,BO.延长BO交⊙O于点E,交AD于点F,连接AE,DE.(1)求证:CD是⊙O的切线;
(2)若AE=DE=3,求AF的长.
分析 (1)欲证明CD是⊙O的切线,只要证明∠CDO=∠CBO=90°,由△COB≌△COD即可解决问题.
(2)先证明∠BAO=∠OAD=∠DAE=∠ABO=30,在Rt△AEF中利用30度性质以及勾股定理即可解决问题.
解答 (1)证明:如图,连接OD.
∵BC为圆O的切线,
∴∠CBD=90°.
∵AO平分∠BAD,
∴∠OAB=∠OBF.
∵OA=OB=OD,
∴∠OAB=∠ABO=∠OAF=∠ODA,
∴∠BOC=∠DOC,
在△COB和△COD中,
$\left\{\begin{array}{l}{CO=CO}\\{∠COB=∠COD}\\{OB=OD}\end{array}\right.$,
∴BOC≌△DOC,
∴∠CBO=∠CDO=90°,
∴CD是⊙O的切线;
(2)∵AE=DE,
∴$\widehat{AE}$=$\widehat{DE}$,
∴∠DAE=∠ABO,
∴∠BAO=∠OAD=∠ABO
∴∠BAO=∠OAD=∠DAE,
∵BE是直径,
∴∠BAE=90°,
∴∠BAO=∠OAD=∠DAE=∠ABO=30°,
∴∠AFE=90°,
在Rt△AFE中,∵AE=3,∠DAE=30°,
∴EF=$\frac{1}{2}$AE=$\frac{3}{2}$,
∴AF=$\sqrt{A{E}^{2}-E{F}^{2}}$=$\frac{3\sqrt{3}}{2}$.
点评 本题考查切线的判定和性质、全等三角形的判定和性质、等边三角形的判定和性质等知识,解题的关键是正确寻找全等三角形,发现特殊角30°,属于中考常考题型.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.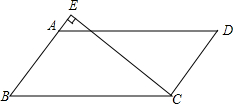 如图,在平行四边形ABCD中,过点C的直线CE⊥AB,垂足为E,若∠EAD=53°,则∠BCE的度数为( )
如图,在平行四边形ABCD中,过点C的直线CE⊥AB,垂足为E,若∠EAD=53°,则∠BCE的度数为( )
 如图,在平行四边形ABCD中,过点C的直线CE⊥AB,垂足为E,若∠EAD=53°,则∠BCE的度数为( )
如图,在平行四边形ABCD中,过点C的直线CE⊥AB,垂足为E,若∠EAD=53°,则∠BCE的度数为( )| A. | 53° | B. | 37° | C. | 47° | D. | 123° |
18.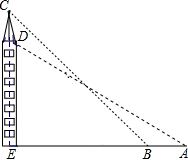 如图,在一个20米高的楼顶上有一信号塔DC,某同学为了测量信号塔的高度,在地面的A处测得信号塔下端D的仰角为30°,然后他正对塔的方向前进了8米到达地面的B处,又测得信号塔顶端C的仰角为45°,CD⊥AB于点E,E、B、A在一条直线上.信号塔CD的高度为( )
如图,在一个20米高的楼顶上有一信号塔DC,某同学为了测量信号塔的高度,在地面的A处测得信号塔下端D的仰角为30°,然后他正对塔的方向前进了8米到达地面的B处,又测得信号塔顶端C的仰角为45°,CD⊥AB于点E,E、B、A在一条直线上.信号塔CD的高度为( )
 如图,在一个20米高的楼顶上有一信号塔DC,某同学为了测量信号塔的高度,在地面的A处测得信号塔下端D的仰角为30°,然后他正对塔的方向前进了8米到达地面的B处,又测得信号塔顶端C的仰角为45°,CD⊥AB于点E,E、B、A在一条直线上.信号塔CD的高度为( )
如图,在一个20米高的楼顶上有一信号塔DC,某同学为了测量信号塔的高度,在地面的A处测得信号塔下端D的仰角为30°,然后他正对塔的方向前进了8米到达地面的B处,又测得信号塔顶端C的仰角为45°,CD⊥AB于点E,E、B、A在一条直线上.信号塔CD的高度为( )| A. | 20$\sqrt{3}$ | B. | 20$\sqrt{3}$-8 | C. | 20$\sqrt{3}$-28 | D. | 20$\sqrt{3}$-20 |
2.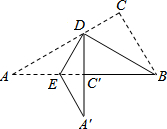 如图的实线部分是由Rt△ABC经过两次折叠得到的,首先将Rt△ABC沿BD折叠,使点C落在斜边上的点C′处,再沿DE折叠使点A落在DC′延长线上的点A′处,若图中,∠A=30°,BC=5cm,则折痕DE的长为( )
如图的实线部分是由Rt△ABC经过两次折叠得到的,首先将Rt△ABC沿BD折叠,使点C落在斜边上的点C′处,再沿DE折叠使点A落在DC′延长线上的点A′处,若图中,∠A=30°,BC=5cm,则折痕DE的长为( )
 如图的实线部分是由Rt△ABC经过两次折叠得到的,首先将Rt△ABC沿BD折叠,使点C落在斜边上的点C′处,再沿DE折叠使点A落在DC′延长线上的点A′处,若图中,∠A=30°,BC=5cm,则折痕DE的长为( )
如图的实线部分是由Rt△ABC经过两次折叠得到的,首先将Rt△ABC沿BD折叠,使点C落在斜边上的点C′处,再沿DE折叠使点A落在DC′延长线上的点A′处,若图中,∠A=30°,BC=5cm,则折痕DE的长为( )| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 2$\sqrt{5}$ | D. | $\frac{10}{3}$ |