题目内容
17.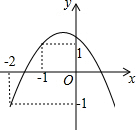 如图,已知关于x的二次函数y=ax2+bx+c的图象经过点(-2,y1),(-1,y2),(1,0),且y1<0<y2,对于以下结论:①abc>0;②a+3b+2c≤0;③a<-$\frac{1}{2}$c;④在-2<x<-1中存在一个实数x0,使得x0=-$\frac{a+b}{a}$,其中正确的个数有( )
如图,已知关于x的二次函数y=ax2+bx+c的图象经过点(-2,y1),(-1,y2),(1,0),且y1<0<y2,对于以下结论:①abc>0;②a+3b+2c≤0;③a<-$\frac{1}{2}$c;④在-2<x<-1中存在一个实数x0,使得x0=-$\frac{a+b}{a}$,其中正确的个数有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 ①正确.画出函数图象即可判断.
②错误.由图象可知,-$\frac{b}{2a}$>-$\frac{1}{2}$,推出b>a,故b-a可以是正数,所以a+3b+2c=a+3b-2a-2b=b-a>0,故错误.
③正确.由a<0,得到b>a,得到a-b<0,推出a-b=a-(-a-c)=2a+c<0,于是得到结论;
④令y=0则ax2+bx-a-b=0,设它的两个根为x1,1,则x1•1=$\frac{-a-b}{a}$=-$\frac{a+b}{a}$,求出x1即可解决问题.
解答 解:由题意二次函数图象如图所示,
∴a<0.b<0,c>0,
∴abc>0,故①正确.
∵-$\frac{b}{2a}$>-$\frac{1}{2}$,
∵a<0,
∴b>a,
∴b-a>0,
∵a+b+c=0,
∴c=-a-b,
∴a+3b+2c=a+3b-2a-2b=b-a>0,
∴a+3b+2c≤0,故②错误.
∵a<0,
∴b>a,
∴a-b<0,
∵a+b+c=0,
∴b=-a-c,
∴a-b=a-(-a-c)=2a+c<0,
∴a+$\frac{1}{2}$c<0,
∴a<-$\frac{1}{2}$c;故③正确;
∵y=ax2+bx+c的图象经过点(1,0),
∴a+b+c=0,
∴c=-a-b,
令y=0则ax2+bx-a-b=0,设它的两个根为x1,1,
∵x1•1=$\frac{-a-b}{a}$=-$\frac{a+b}{a}$,
∴x1=-$\frac{a+b}{a}$,
∵-2<x1<x2,
∴在-2<x<-1中存在一个实数x0,使得x0=-$\frac{a+b}{a}$,故④正确,
故选D.
点评 本题考查二次函数的图象与系数的关系、二次函数图象上的点的坐标特征,解题的关键是灵活应用二次函数的性质解决问题,学会构建二次函数解决最值问题,属于中考填空题中的压轴题.

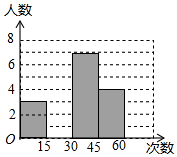 在大课间活动中,体育老师随机抽取了七年级甲、乙两班部分女学生进行仰卧起坐的测试,并对成绩进行统计分析,绘制了频数分布表和统计图,请你根据图表中的信息完成下列问题:
在大课间活动中,体育老师随机抽取了七年级甲、乙两班部分女学生进行仰卧起坐的测试,并对成绩进行统计分析,绘制了频数分布表和统计图,请你根据图表中的信息完成下列问题:| 分 组 | 频数 | 频率 |
| 第一组(0≤x<15) | 3 | 0.15 |
| 第二组(15≤x<30) | a | 0.3 |
| 第三组(30≤x<45) | 7 | 0.35 |
| 第四组(45≤x<60) | 4 | b |
(2)已知第一组中只有一个甲班学生,第四组中只有一个乙班学生,老师随机从这两个组中各选一名学生谈心得体会,则所选两人正好都是甲班学生的概率是多少?
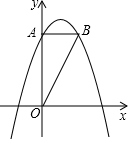 如图,已知抛物线y=ax2+bx+4经过点(2,4),(-2,-2),交y轴于点A,过点A作AB⊥y轴交抛物线于点B.
如图,已知抛物线y=ax2+bx+4经过点(2,4),(-2,-2),交y轴于点A,过点A作AB⊥y轴交抛物线于点B.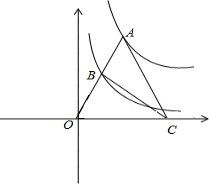 如图,点A为函数$y=\frac{18}{x}(x>0)$图象上一点,连结OA,交函数$y=\frac{2}{x}(x>0)$的图象于点B,点C是x轴上一点,且AO=AC,求△ABC的面积.
如图,点A为函数$y=\frac{18}{x}(x>0)$图象上一点,连结OA,交函数$y=\frac{2}{x}(x>0)$的图象于点B,点C是x轴上一点,且AO=AC,求△ABC的面积.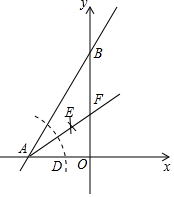 如图,在平面直角坐标系中,一次函数y=$\sqrt{3}$x+1的图象分别与x轴、y轴交于A、B两点,以A为圆心,适当长为半径画弧分别交AB、AO于点C、D,再分别以C、D为圆心,大于$\frac{1}{2}$CD的长为半径画弧,两弧交于点E,连接AE并延长交y轴于点F,则下列说法正确的个数是( )
如图,在平面直角坐标系中,一次函数y=$\sqrt{3}$x+1的图象分别与x轴、y轴交于A、B两点,以A为圆心,适当长为半径画弧分别交AB、AO于点C、D,再分别以C、D为圆心,大于$\frac{1}{2}$CD的长为半径画弧,两弧交于点E,连接AE并延长交y轴于点F,则下列说法正确的个数是( )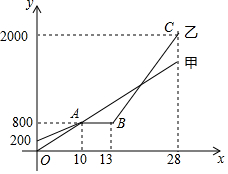 甲、乙相约去离家2000m的公园晨练,甲先出发一直匀速前行,乙后出发,如图是甲和乙所走的路程s(m)与时间t(min)的函数图象.
甲、乙相约去离家2000m的公园晨练,甲先出发一直匀速前行,乙后出发,如图是甲和乙所走的路程s(m)与时间t(min)的函数图象.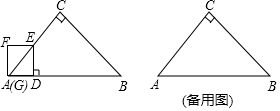
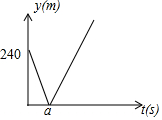 甲,乙两人沿同一条滨海大道同起点、同方向进行体育锻炼,已知甲匀速跑步,先出发60s,乙匀速骑车,速度是甲的两倍,在锻炼的过程中,设甲乙两人相距y(m),乙骑车的时间为t(s),y是t的函数,其图象的一部分如图所示.
甲,乙两人沿同一条滨海大道同起点、同方向进行体育锻炼,已知甲匀速跑步,先出发60s,乙匀速骑车,速度是甲的两倍,在锻炼的过程中,设甲乙两人相距y(m),乙骑车的时间为t(s),y是t的函数,其图象的一部分如图所示.