题目内容
7.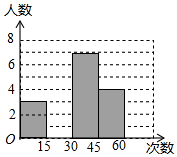 在大课间活动中,体育老师随机抽取了七年级甲、乙两班部分女学生进行仰卧起坐的测试,并对成绩进行统计分析,绘制了频数分布表和统计图,请你根据图表中的信息完成下列问题:
在大课间活动中,体育老师随机抽取了七年级甲、乙两班部分女学生进行仰卧起坐的测试,并对成绩进行统计分析,绘制了频数分布表和统计图,请你根据图表中的信息完成下列问题:| 分 组 | 频数 | 频率 |
| 第一组(0≤x<15) | 3 | 0.15 |
| 第二组(15≤x<30) | a | 0.3 |
| 第三组(30≤x<45) | 7 | 0.35 |
| 第四组(45≤x<60) | 4 | b |
(2)已知第一组中只有一个甲班学生,第四组中只有一个乙班学生,老师随机从这两个组中各选一名学生谈心得体会,则所选两人正好都是甲班学生的概率是多少?
分析 (1)由统计图易得a与b的值,继而将统计图补充完整;
(2)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与所选两人正好都是甲班学生的情况,再利用概率公式即可求得答案.
解答 解:(1)b=1-0.15-0.35-0.30=0.2;
∵总人数为:3÷0.15=20(人),
∴a=20×0.30=6(人);
故答案为:6,0.2;
补全统计图得:
(2)画树状图得:
∵共有12种等可能的结果,所选两人正好都是甲班学生的有3种情况,
∴所选两人正好都是甲班学生的概率是:$\frac{3}{12}$=$\frac{1}{4}$.
点评 此题考查了列表法或树状图法求概率以及条形统计图的知识.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
15.某校举办诗词大会有4名女生和6名男生获奖,现从中任选1人去参加区诗词大会,则选中女生的概率是( )
| A. | $\frac{1}{10}$ | B. | $\frac{3}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{4}$ |
12.某水果店在两周内,将标价为10元/斤的某种水果,经过两次降价后的价格为8.1元/斤,并且两次降价的百分率相同.
(1)求该种水果每次降价的百分率;
(2)从第一次降价的第1天算起,第x天(x为整数)的售价、销量及储存和损耗费用的相关信息如表所示.已知该种水果的进价为4.1元/斤,设销售该水果第x(天)的利润为y(元),求y与x(1≤x<15)之间的函数关系式,并求出第几天时销售利润最大?
(3)在(2)的条件下,若要使第15天的利润比(2)中最大利润最多少127.5元,则第15天在第14天的价格基础上最多可降多少元?
(1)求该种水果每次降价的百分率;
(2)从第一次降价的第1天算起,第x天(x为整数)的售价、销量及储存和损耗费用的相关信息如表所示.已知该种水果的进价为4.1元/斤,设销售该水果第x(天)的利润为y(元),求y与x(1≤x<15)之间的函数关系式,并求出第几天时销售利润最大?
| 时间x(天) | 1≤x<9 | 9≤x<15 | x≥15 |
| 售价(元/斤) | 第1次降价后的价格 | 第2次降价后的价格 | |
| 销量(斤) | 80-3x | 120-x | |
| 储存和损耗费用(元) | 40+3x | 3x2-64x+400 | |
16.某商店分两次购进 A、B两种商品进行销售,两次购进同一种商品的进价相同,具体情况如下表所示:
(1)求A、B两种商品每件的进价分别是多少元?
(2)商场决定A种商品以每件30元出售,B种商品以每件100元出售.为满足市场需求,需购进A、B两种商品共1000件,且A种商品的数量不少于B种商品数量的4倍,请你求出获利最大的进货方案,并确定最大利润.
| 购进数量(件) | 购进所需费用(元) | ||
| A | B | ||
| 第一次 | 30 | 40 | 3800 |
| 第二次 | 40 | 30 | 3200 |
(2)商场决定A种商品以每件30元出售,B种商品以每件100元出售.为满足市场需求,需购进A、B两种商品共1000件,且A种商品的数量不少于B种商品数量的4倍,请你求出获利最大的进货方案,并确定最大利润.
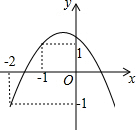 如图,已知关于x的二次函数y=ax2+bx+c的图象经过点(-2,y1),(-1,y2),(1,0),且y1<0<y2,对于以下结论:①abc>0;②a+3b+2c≤0;③a<-$\frac{1}{2}$c;④在-2<x<-1中存在一个实数x0,使得x0=-$\frac{a+b}{a}$,其中正确的个数有( )
如图,已知关于x的二次函数y=ax2+bx+c的图象经过点(-2,y1),(-1,y2),(1,0),且y1<0<y2,对于以下结论:①abc>0;②a+3b+2c≤0;③a<-$\frac{1}{2}$c;④在-2<x<-1中存在一个实数x0,使得x0=-$\frac{a+b}{a}$,其中正确的个数有( )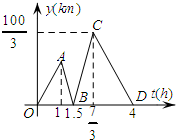 甲开汽车,乙骑自行车从M地出发沿一条公路匀速前往N地,设乙行驶的时间为t(h),甲乙两人之间的距离为y(km),y与t的函数关系如图所示,已知乙比甲先出发1h.
甲开汽车,乙骑自行车从M地出发沿一条公路匀速前往N地,设乙行驶的时间为t(h),甲乙两人之间的距离为y(km),y与t的函数关系如图所示,已知乙比甲先出发1h.
 如图,点O是线段AB上一点,AB=4cm,AO=1cm,若线段AB绕点O顺时针旋转120°到线段A′B′的位置,则线段AB在旋转过程中扫过的图形的面积为$\frac{4π}{3}$cm2.(结果保留π)
如图,点O是线段AB上一点,AB=4cm,AO=1cm,若线段AB绕点O顺时针旋转120°到线段A′B′的位置,则线段AB在旋转过程中扫过的图形的面积为$\frac{4π}{3}$cm2.(结果保留π)