题目内容
9.如图,在Rt△ABC中,∠C=90°,AC=BC,AB=4cm,线段AB上一动点D,以1cm/s的速度从点A出发向终点B运动.过点D作DE⊥AB,交折线AC-CB于点E,以DE为一边,在DE左侧作正方形DEFG.设运动时间为x(s)(0<x<4).正方形DEFG与△ABC重叠部分面积为y(cm2).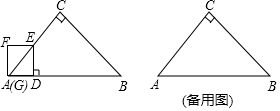
(1)当x=$\frac{8}{3}$s时,点F在AC上;
(2)求y关于x的函数解析式,并写出自变量x的取值范围;
(3)设正方形DEFG的中心为点O,直接写出运动过程中,直线BO平分△ABC面积时,自变量x的取值范围.
分析 (1)如图1中,当点F在AB上时,易证AG=GE=DG=DB=$\frac{4}{3}$,由此求出AD的长即可解决问题;
(2)分三种情形讨论:①如图2中,当0<x≤2时,重叠部分是△ADE,②如图3中,当2<x≤$\frac{8}{3}$时,重叠部分是五边形MNEDG.③当$\frac{8}{3}$<x<4时,重叠部分是正方形DEFG,分别求解即可解决问题;
(3)如图5中,当2≤x<4时,延长BO交AC于M.只要证明CM=AM即可解决问题;
解答 解:(1)如图1中,当点F在AB上时,易证AG=GE=DG=DB=$\frac{4}{3}$,
∴运动时间x=$\frac{AD}{1}$=$\frac{8}{3}$,
故答案为$\frac{8}{3}$.
(2)①如图2中,当0<x≤2时,重叠部分是△ADE,
∵∠C=90°,AC=BC,
∴∠CAB=∠AED=45°,
∴AD=DE=x,
∴y=S△ADE=$\frac{1}{2}$x2,
②如图3中,当2<x≤$\frac{8}{3}$时,重叠部分是五边形MNEDG.
易知FG=GD=DE=DB=4-x,MG=AG=x-(4-x)=2x-4,
∴FM=FG-MG=(4-x)-(2x-4)=8-3x=FN,
∴y=S正方形DEFG-S△FMN=(4-x)2-$\frac{1}{2}$(8-3x)2=-$\frac{7}{2}$x2+16x-16,
③当$\frac{8}{3}$<x<4时,重叠部分是正方形DEFG,
y=(4-x)2=x2-8x+16.
综上所述,y=$\left\{\begin{array}{l}{\frac{1}{2}{x}^{2}}&{(0<x≤2)}\\{-\frac{7}{2}{x}^{2}+16x-16}&{(2<x≤\frac{8}{3})}\\{{x}^{2}-8x+16}&{(\frac{8}{3}<x<4)}\end{array}\right.$
(3)如图5中,当2≤x<4时,延长BO交AC于M.
∵OE=OG,EG∥AC,
∴$\frac{OE}{CM}$=$\frac{BO}{BM}$=$\frac{OG}{AM}$,
∴CM=AM,
∴直线OB平分△ABC的面积.
∴当2≤x<4时,直线OB平分△ABC的面积.
点评 本题考查四边形综合题、正方形的性质、等腰直角三角形的性质、三角形的中线的性质等知识,解题的关键是灵活运用所学知识解决问题,学会用分类讨论的思想思考问题,属于中考压轴题.

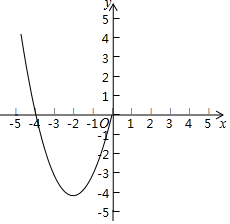 某数学兴趣小组对函数y=x2-4|x|的图象和性质进行探究,发现自变量x的取值范围是全体实数,x与y的几组对应值列表如下:
某数学兴趣小组对函数y=x2-4|x|的图象和性质进行探究,发现自变量x的取值范围是全体实数,x与y的几组对应值列表如下:| x | … | -3 | -2 | -1 | 0 | 1 | 2 | 3 | … |
| y | … | -3 | -4 | -3 | 0 | -3 | … |
(2)根据表中数据,画出函数图象的另一部分;
(3)进一步探究函数图象,回答问题:
①观察图象可以得出,对应的方程x2-4|x|=0有3个实数根;
②关于x的方程x2-4|x|=a有2个实数根时,a的取值范围是a=-4或a>0;
③当x取何值时,y随x的增大而增大?
| A. | k>0 | B. | k<2 | C. | 0<k<2 | D. | -2<k<0 |
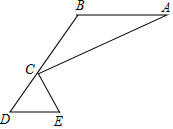 如图,AB∥DE,C为BD上一点,∠A=∠BCA,∠E=∠ECD,求证:CE⊥CA.
如图,AB∥DE,C为BD上一点,∠A=∠BCA,∠E=∠ECD,求证:CE⊥CA.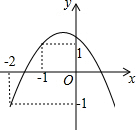 如图,已知关于x的二次函数y=ax2+bx+c的图象经过点(-2,y1),(-1,y2),(1,0),且y1<0<y2,对于以下结论:①abc>0;②a+3b+2c≤0;③a<-$\frac{1}{2}$c;④在-2<x<-1中存在一个实数x0,使得x0=-$\frac{a+b}{a}$,其中正确的个数有( )
如图,已知关于x的二次函数y=ax2+bx+c的图象经过点(-2,y1),(-1,y2),(1,0),且y1<0<y2,对于以下结论:①abc>0;②a+3b+2c≤0;③a<-$\frac{1}{2}$c;④在-2<x<-1中存在一个实数x0,使得x0=-$\frac{a+b}{a}$,其中正确的个数有( )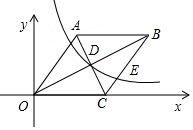 如图,菱形OABC的边OC在x轴正半轴上,点B的坐标为(8,4).
如图,菱形OABC的边OC在x轴正半轴上,点B的坐标为(8,4).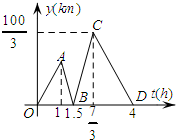 甲开汽车,乙骑自行车从M地出发沿一条公路匀速前往N地,设乙行驶的时间为t(h),甲乙两人之间的距离为y(km),y与t的函数关系如图所示,已知乙比甲先出发1h.
甲开汽车,乙骑自行车从M地出发沿一条公路匀速前往N地,设乙行驶的时间为t(h),甲乙两人之间的距离为y(km),y与t的函数关系如图所示,已知乙比甲先出发1h. 如图,点O是线段AB上一点,AB=4cm,AO=1cm,若线段AB绕点O顺时针旋转120°到线段A′B′的位置,则线段AB在旋转过程中扫过的图形的面积为$\frac{4π}{3}$cm2.(结果保留π)
如图,点O是线段AB上一点,AB=4cm,AO=1cm,若线段AB绕点O顺时针旋转120°到线段A′B′的位置,则线段AB在旋转过程中扫过的图形的面积为$\frac{4π}{3}$cm2.(结果保留π)