题目内容
5.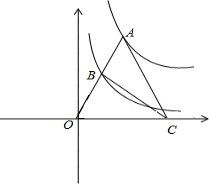 如图,点A为函数$y=\frac{18}{x}(x>0)$图象上一点,连结OA,交函数$y=\frac{2}{x}(x>0)$的图象于点B,点C是x轴上一点,且AO=AC,求△ABC的面积.
如图,点A为函数$y=\frac{18}{x}(x>0)$图象上一点,连结OA,交函数$y=\frac{2}{x}(x>0)$的图象于点B,点C是x轴上一点,且AO=AC,求△ABC的面积.
分析 根据题意可以分别设出点A、点B的坐标,根据点O、A、B在同一条直线上可以得到A、B的坐标之间的关系,由AO=AC可知点C的横坐标是点A的横坐标的2倍,从而可以得到△ABC的面积.
解答 解:设点A的坐标为(a,$\frac{18}{a}$),点B的坐标为(b,$\frac{2}{b}$),
∵点C是x轴上一点,且AO=AC,
∴点C的坐标是(2a,0),
设过点O(0,0),A(a,$\frac{18}{a}$)的直线的解析式为:y=kx,
∴$\frac{18}{a}$=ak,
解得,k=$\frac{18}{{a}^{2}}$,
又∵点B(b,$\frac{2}{b}$)在y=$\frac{18}{{a}^{2}}$x上,
∴$\frac{2}{b}$=$\frac{18}{{a}^{2}}$•b,解得,$\frac{a}{b}$=3或$\frac{a}{b}$=-3(舍去),
∴S△ABC=S△AOC-S△OBC=$\frac{2a•\frac{18}{a}}{2}$-$\frac{2a•\frac{2}{b}}{2}$=18-6=12.
点评 本题考查反比例函数的图象、三角形的面积、等腰三角形的性质,解题的关键是明确题意,找出所求问题需要的条件.

练习册系列答案
相关题目
16.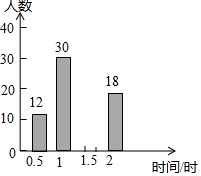 在西安市开展“美丽城市,创卫同行”活动中,我校倡议七年级学生利用双休日在各自社区参加义务劳动,为了解同学们劳动情况,学校随机调查了部分同学的劳动时间,并用得到的数据绘制不完整的统计图表,如图所示:
在西安市开展“美丽城市,创卫同行”活动中,我校倡议七年级学生利用双休日在各自社区参加义务劳动,为了解同学们劳动情况,学校随机调查了部分同学的劳动时间,并用得到的数据绘制不完整的统计图表,如图所示:
(1)统计表中的m=100,x=40,y=0.18.
(2)被调查同学劳动时间的中位数是1.5;
(3)请将频数分布直方图补充完整.
 在西安市开展“美丽城市,创卫同行”活动中,我校倡议七年级学生利用双休日在各自社区参加义务劳动,为了解同学们劳动情况,学校随机调查了部分同学的劳动时间,并用得到的数据绘制不完整的统计图表,如图所示:
在西安市开展“美丽城市,创卫同行”活动中,我校倡议七年级学生利用双休日在各自社区参加义务劳动,为了解同学们劳动情况,学校随机调查了部分同学的劳动时间,并用得到的数据绘制不完整的统计图表,如图所示:| 劳动时间(时)0.5 | 频数(人数)12 | 频率0.12 |
| 1 | 30 | 0.3 |
| 1.5 | x | 0.4 |
| 2 | 18 | y |
| 合计 | m | 1 |
(2)被调查同学劳动时间的中位数是1.5;
(3)请将频数分布直方图补充完整.
20.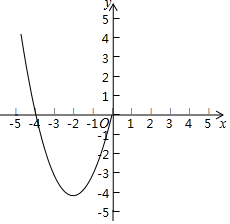 某数学兴趣小组对函数y=x2-4|x|的图象和性质进行探究,发现自变量x的取值范围是全体实数,x与y的几组对应值列表如下:
某数学兴趣小组对函数y=x2-4|x|的图象和性质进行探究,发现自变量x的取值范围是全体实数,x与y的几组对应值列表如下:
(1)补全上表;
(2)根据表中数据,画出函数图象的另一部分;
(3)进一步探究函数图象,回答问题:
①观察图象可以得出,对应的方程x2-4|x|=0有3个实数根;
②关于x的方程x2-4|x|=a有2个实数根时,a的取值范围是a=-4或a>0;
③当x取何值时,y随x的增大而增大?
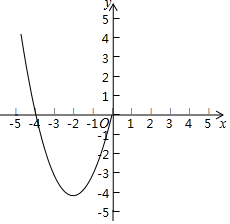 某数学兴趣小组对函数y=x2-4|x|的图象和性质进行探究,发现自变量x的取值范围是全体实数,x与y的几组对应值列表如下:
某数学兴趣小组对函数y=x2-4|x|的图象和性质进行探究,发现自变量x的取值范围是全体实数,x与y的几组对应值列表如下:| x | … | -3 | -2 | -1 | 0 | 1 | 2 | 3 | … |
| y | … | -3 | -4 | -3 | 0 | -3 | … |
(2)根据表中数据,画出函数图象的另一部分;
(3)进一步探究函数图象,回答问题:
①观察图象可以得出,对应的方程x2-4|x|=0有3个实数根;
②关于x的方程x2-4|x|=a有2个实数根时,a的取值范围是a=-4或a>0;
③当x取何值时,y随x的增大而增大?
14.已知直线y=$\frac{1}{2}$x+k-4与抛物线y=x2-4kx-3k+4k2的对称轴的交点在第四象限,则k的取值范围是( )
| A. | k>0 | B. | k<2 | C. | 0<k<2 | D. | -2<k<0 |
15.某校举办诗词大会有4名女生和6名男生获奖,现从中任选1人去参加区诗词大会,则选中女生的概率是( )
| A. | $\frac{1}{10}$ | B. | $\frac{3}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{4}$ |
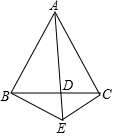 如图,在△ABC中,AB=AC,AD平分∠BAC,E是AD的延长线上任意一点,连接BE,CE.则四边形ABEC是轴对称图形吗?请简单说明理由.
如图,在△ABC中,AB=AC,AD平分∠BAC,E是AD的延长线上任意一点,连接BE,CE.则四边形ABEC是轴对称图形吗?请简单说明理由.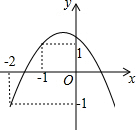 如图,已知关于x的二次函数y=ax2+bx+c的图象经过点(-2,y1),(-1,y2),(1,0),且y1<0<y2,对于以下结论:①abc>0;②a+3b+2c≤0;③a<-$\frac{1}{2}$c;④在-2<x<-1中存在一个实数x0,使得x0=-$\frac{a+b}{a}$,其中正确的个数有( )
如图,已知关于x的二次函数y=ax2+bx+c的图象经过点(-2,y1),(-1,y2),(1,0),且y1<0<y2,对于以下结论:①abc>0;②a+3b+2c≤0;③a<-$\frac{1}{2}$c;④在-2<x<-1中存在一个实数x0,使得x0=-$\frac{a+b}{a}$,其中正确的个数有( )