题目内容
9.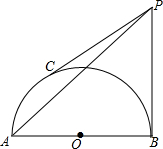 如图,AB为半圆O的直径,C为半圆弧上的三等分点,半圆O的切线PB和PC相交于点P,若AB=4cm,求PA的长.
如图,AB为半圆O的直径,C为半圆弧上的三等分点,半圆O的切线PB和PC相交于点P,若AB=4cm,求PA的长.
分析 直接利用三等分点的定义得出∠AOC=∠COP=∠BOP=60°,进而利用锐角三角函数关系得出PB的长,再利用勾股定理得出PA的长.
解答 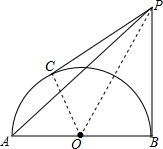 解:连接CO,PO,
解:连接CO,PO,
∵AB为半圆O的直径,C为半圆弧上的三等分点,
∴∠AOC=∠COP=∠BOP=60°,
∵半圆O的切线PB和PC相交于点P,
∴∠PBO=90°,
∵AB=4cm,
∴BO=2cm,
∴tan60°=$\frac{PB}{2}$=$\sqrt{3}$,
解得:PB=2$\sqrt{3}$,
∴PA=$\sqrt{(2\sqrt{3})^{2}+{4}^{2}}$=2$\sqrt{7}$(cm).
点评 此题主要考查了切线的性质以及勾股定理等知识,根据题意得出PB的长是解题关键.

练习册系列答案
相关题目
4.下列各点,在抛物线y=(x-2)2+2上的点是( )
| A. | (0,4) | B. | (2,0) | C. | (2,2) | D. | (0,-2) |
14.已知⊙O的半径为4cm,直线l与⊙O相切,则圆心O与直线l的距离为( )
| A. | 2cm | B. | 4cm | C. | 8cm | D. | 无法确定 |
19.下列运算结果为-a8的是( )
| A. | (-a)3+(-a)5 | B. | (-a)3•(-a)5 | C. | (-a3)5 | D. | (-a)10÷(-a2) |
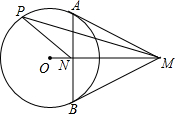 M为圆O外一定点,MA、MB是圆O的两条切线,AB与OM交于N,P为圆O上一动点,求证:$\frac{PN}{PM}$为定值.
M为圆O外一定点,MA、MB是圆O的两条切线,AB与OM交于N,P为圆O上一动点,求证:$\frac{PN}{PM}$为定值. 如图,△ABC的三个顶点别为A(1,4),B(5,1),C(1,9),若双曲线y=$\frac{k}{x}$(x>0)在第一象限内与△ABC有交点,求k的取值范围.
如图,△ABC的三个顶点别为A(1,4),B(5,1),C(1,9),若双曲线y=$\frac{k}{x}$(x>0)在第一象限内与△ABC有交点,求k的取值范围.