题目内容
1.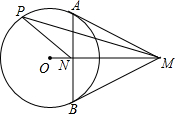 M为圆O外一定点,MA、MB是圆O的两条切线,AB与OM交于N,P为圆O上一动点,求证:$\frac{PN}{PM}$为定值.
M为圆O外一定点,MA、MB是圆O的两条切线,AB与OM交于N,P为圆O上一动点,求证:$\frac{PN}{PM}$为定值.
分析 连接OP,OB,根据切线的性质得到AM=BM,∠AMO=∠BMO,推出△BON∽△MOB,根据相似三角形的性质得到$\frac{OB}{OM}=\frac{ON}{OB}$,等量代换得到$\frac{OP}{OM}=\frac{ON}{OP}$,通过△POM∽△NOP,得到$\frac{PM}{PN}=\frac{OM}{OP}=\frac{OM}{OB}$,即可得到结论.
解答 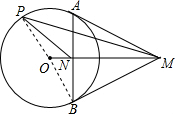 解:连接OP,OB,
解:连接OP,OB,
∵MA、MB是圆O的两条切线,
∴AM=BM,∠AMO=∠BMO,
∴OM⊥AB,OB⊥MB,
∴∠ONB=∠OBM=90°,∠BON=∠MOB,
∴△BON∽△MOB,
∴$\frac{OB}{OM}=\frac{ON}{OB}$,
∵OP=OB,
∴$\frac{OP}{OM}=\frac{ON}{OP}$,
∵∠POM=∠NOP,
∴△POM∽△NOP,
∴$\frac{PM}{PN}=\frac{OM}{OP}=\frac{OM}{OB}$,
∵OM,OB为定值,
∴$\frac{PN}{PM}$为定值.
点评 本题考查了切线的性质,相似三角形的判定和性质,正确的作出辅助线是解题的关键.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案
相关题目
6.反比例函数y=(2m-1)${x}^{{m}^{2}-1}$,当x>0时,y随x的增大而增大,则m的值是( )
| A. | ±1 | B. | 小于$\frac{1}{2}$的实数 | C. | -1 | D. | 1 |
10.将正整数1,2,3,4…按以下方式排列

根据排列规律,从2015到2017的箭头依次为( )

根据排列规律,从2015到2017的箭头依次为( )
| A. | ↓→ | B. | →↓ | C. | ↑→ | D. | →↑ |
11.若有理数a和b在数轴上所表示的点分别在原点的右边和左边,则|b|-|a-b|等于( )
| A. | a | B. | -a | C. | 2b+a | D. | 2b-a |
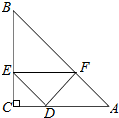 如图,在等腰直角△ABC中,∠C=90°,AC=10,点D为AC边的一个动点(不与点A、C重合),过点D作DE∥AB,交BC于点E,再过点E作EF∥AC,交AB于点F.
如图,在等腰直角△ABC中,∠C=90°,AC=10,点D为AC边的一个动点(不与点A、C重合),过点D作DE∥AB,交BC于点E,再过点E作EF∥AC,交AB于点F.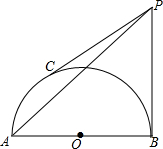 如图,AB为半圆O的直径,C为半圆弧上的三等分点,半圆O的切线PB和PC相交于点P,若AB=4cm,求PA的长.
如图,AB为半圆O的直径,C为半圆弧上的三等分点,半圆O的切线PB和PC相交于点P,若AB=4cm,求PA的长. 已知:如图,动点P在函数y=$\frac{k}{x}$(x>0)的图象上运动,PM⊥x轴于M,PN⊥y轴于N,线段PM、PN分别与直线AB:y=-x+1交于点E、F,且AF•BE的值为1,则k为$\frac{1}{2}$.
已知:如图,动点P在函数y=$\frac{k}{x}$(x>0)的图象上运动,PM⊥x轴于M,PN⊥y轴于N,线段PM、PN分别与直线AB:y=-x+1交于点E、F,且AF•BE的值为1,则k为$\frac{1}{2}$.