题目内容
13．先化简，再求值：$\frac{{x}^{2}-1}{{x}^{2}-x-2}$+$\frac{x}{2x-4}$，其中x=$\frac{1}{2}$．分析 原式约分后两项通分，并利用同分母分式的加法法则计算，得到最简结果，把x的值代入计算即可求出值．
解答 解：原式=$\frac{（x+1）（x-1）}{（x-2）（x+1）}$+$\frac{x}{2（x-2）}$=$\frac{x-1}{x-2}$+$\frac{x}{2（x-2）}$=$\frac{3x-2}{2（x-2）}$，
当x=$\frac{1}{2}$时，原式=$\frac{\frac{3}{2}-2}{2×（-\frac{3}{2}）}$=$\frac{1}{6}$．
点评 此题考查了分式的化简求值，熟练掌握运算法则是解本题的关键．
练习册系列答案
活力课时同步练习册系列答案
学业测评一课一测系列答案
相关题目
5．设a≠b，m≠n，a，b，m，n是已知数，则方程组$\left\{\begin{array}{l}\frac{x}{a+m}+\frac{y}{b+m}=1\\ \frac{x}{a+n}+\frac{y}{b+n}=1\end{array}\right.$的解是（ ）
| A． | $\left\{\begin{array}{l}x=\frac{（a+m）（a+n）}{a+b}\\ y=\frac{（b+m）（b+n）}{a+b}\end{array}\right.$ | B． | $\left\{\begin{array}{l}x=\frac{（a+m）（b+m）}{a-b}\\ y=\frac{（a+n）（b+n）}{a-b}\end{array}\right.$ | ||
| C． | $\left\{\begin{array}{l}x=\frac{（a+m）（a+n）}{a-b}\\ y=\frac{（b+m）（b+n）}{a-b}\end{array}\right.$ | D． | $\left\{\begin{array}{l}x=\frac{（a+m）（a+n）}{a-b}\\ y=-\frac{（b+m）（b+n）}{a-b}\end{array}\right.$ |
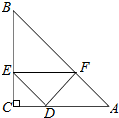如图，在等腰直角△ABC中，∠C=90°，AC=10，点D为AC边的一个动点（不与点A、C重合），过点D作DE∥AB，交BC于点E，再过点E作EF∥AC，交AB于点F．
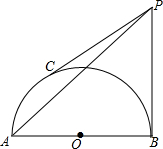如图，AB为半圆O的直径，C为半圆弧上的三等分点，半圆O的切线PB和PC相交于点P，若AB=4cm，求PA的长．
10．将正整数1，2，3，4…按以下方式排列
根据排列规律，从2015到2017的箭头依次为（ ）
根据排列规律，从2015到2017的箭头依次为（ ）
| A． | ↓→ | B． | →↓ | C． | ↑→ | D． | →↑ |