题目内容
12．解不等式组$\left\{\begin{array}{l}{2（x+3）≥3-x}\\{3-\frac{x+1}{4}＞2}\end{array}\right.$，并将解集在数轴上表示出来．分析 分别求出不等式组中两不等式的解集，找出解集的公共部分确定出不等式组的解集，表示在数轴上即可．
解答 解：$\left\{\begin{array}{l}{2（x+3）≥3-x①}\\{3-\frac{x+1}{4}＞2②}\end{array}\right.$，
由①得：x≥-1，
由②得：x＜3，
则不等式组的解集为-1≤x＜3，
表示在数轴上，如图所示，
点评 此题考查了解一元一次不等式组，以及在数轴上表示不等式的解集，熟练掌握运算法则是解本题的关键．
练习册系列答案
相关题目
2．
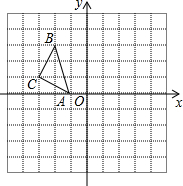如图，在平面直角坐标系中，△ABC的三个顶点的坐标分别为A（-1，0），B（-2，3），C（-3，1）．将△ABC沿y轴翻折得到△A′B′C′，则点B′的坐标为（ ）
如图，在平面直角坐标系中，△ABC的三个顶点的坐标分别为A（-1，0），B（-2，3），C（-3，1）．将△ABC沿y轴翻折得到△A′B′C′，则点B′的坐标为（ ）| A． | （2，1） | B． | （2，3） | C． | （4，1） | D． | （0，2） |
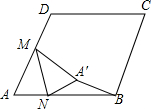如图，在边长为2的菱形ABCD中，∠A=60°，M是AD边的中点，N是AB边上的一动点，将△AMN沿MN所在直线翻折得到△A′MN，连接A′B，请求出A′B长度的最小值．
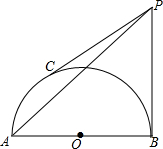如图，AB为半圆O的直径，C为半圆弧上的三等分点，半圆O的切线PB和PC相交于点P，若AB=4cm，求PA的长．