题目内容
14.已知⊙O的半径为4cm,直线l与⊙O相切,则圆心O与直线l的距离为( )| A. | 2cm | B. | 4cm | C. | 8cm | D. | 无法确定 |
分析 连接OP,根据切线的性质得出OP⊥AB,根据垂线段最短得出OP的长最短,得出选项即可.
解答 解:连接OP,
∵直线AB切⊙O于P,
∴OP⊥AB,
即OP的长是圆心到直线的最短距离,
∴OP=4cm,
故选B.
点评 本题考查了点到直线的距离,切线的性质,直线和圆的位置关系的应用,解此题的关键是找出OP的位置,难度适中.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
5.设a≠b,m≠n,a,b,m,n是已知数,则方程组$\left\{\begin{array}{l}\frac{x}{a+m}+\frac{y}{b+m}=1\\ \frac{x}{a+n}+\frac{y}{b+n}=1\end{array}\right.$的解是( )
| A. | $\left\{\begin{array}{l}x=\frac{(a+m)(a+n)}{a+b}\\ y=\frac{(b+m)(b+n)}{a+b}\end{array}\right.$ | B. | $\left\{\begin{array}{l}x=\frac{(a+m)(b+m)}{a-b}\\ y=\frac{(a+n)(b+n)}{a-b}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}x=\frac{(a+m)(a+n)}{a-b}\\ y=\frac{(b+m)(b+n)}{a-b}\end{array}\right.$ | D. | $\left\{\begin{array}{l}x=\frac{(a+m)(a+n)}{a-b}\\ y=-\frac{(b+m)(b+n)}{a-b}\end{array}\right.$ |
6.反比例函数y=(2m-1)${x}^{{m}^{2}-1}$,当x>0时,y随x的增大而增大,则m的值是( )
| A. | ±1 | B. | 小于$\frac{1}{2}$的实数 | C. | -1 | D. | 1 |
4.下列各组数中,互为相反数的一组是( )
| A. | -2与$\sqrt{(-2)^{2}}$ | B. | -2与$\root{3}{-8}$ | C. | 2与$\sqrt{-4}$ | D. | $\sqrt{1{0}^{-4}}$与2 |
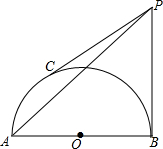 如图,AB为半圆O的直径,C为半圆弧上的三等分点,半圆O的切线PB和PC相交于点P,若AB=4cm,求PA的长.
如图,AB为半圆O的直径,C为半圆弧上的三等分点,半圆O的切线PB和PC相交于点P,若AB=4cm,求PA的长.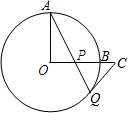 如图,已知⊙O的半径OA⊥OB,过点A的直线交OB于点P,交⊙O于点Q,过Q点引⊙O的切线交OB的延长线于点C,求证:CP=CQ.
如图,已知⊙O的半径OA⊥OB,过点A的直线交OB于点P,交⊙O于点Q,过Q点引⊙O的切线交OB的延长线于点C,求证:CP=CQ.