题目内容
18. 如图,在△ABC中,AD⊥BC,CE⊥AB,垂足分别为点D、E.若BE=2AE,AD=3,tan∠BCE=$\frac{\sqrt{3}}{3}$,则CE=4.
如图,在△ABC中,AD⊥BC,CE⊥AB,垂足分别为点D、E.若BE=2AE,AD=3,tan∠BCE=$\frac{\sqrt{3}}{3}$,则CE=4.
分析 根据tan∠BCE=$\frac{\sqrt{3}}{3}$,确定∠BCE=30°,则∠B=60°.在Rt△ABD和Rt△BEC中求解.
解答 解:∵tan∠BCE=$\frac{\sqrt{3}}{3}$
∴∠BCE=30°
∴∠B=60°
又∵在Rt△ABD中,AD=3,
∴BD=$\sqrt{3}$,AB=2$\sqrt{3}$,
∵BE=2AE
∴BE=$\frac{4\sqrt{3}}{3}$,AE=$\frac{2\sqrt{3}}{3}$,
在Rt△BEC中,BE=$\frac{4\sqrt{3}}{3}$,∠BCE=30°,
∴CE=4.
故答案为:4.
点评 本题考查利用特殊角的三角函数值解直角三角形,题目比较好,难度不大.

练习册系列答案
相关题目
13.非等边三角形的三条边都是方程x2-6x+8=0的解,则这个三角形的周长是( )
| A. | 6 | B. | 8 | C. | 10 | D. | 8 或 10 |
10.如图,水平地面上有一面积为30πcm2的灰色扇形OAB,其中OA=6cm,且OA垂直于地面,将这个扇形向右滚动(无滑动)至点B刚好接触地面为止,则在这个滚动过程中,点O移动的距离是( )
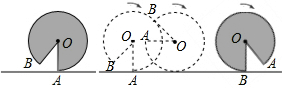

| A. | 10πcm | B. | 20πcm | C. | 24πcm | D. | 30πcm |
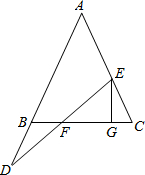 如图,在△ABC中,AB=AC,点E在线段AC上,D在AB的延长线上,连接DE交BC于F,过E作EG⊥BC于G.
如图,在△ABC中,AB=AC,点E在线段AC上,D在AB的延长线上,连接DE交BC于F,过E作EG⊥BC于G.