题目内容
8.观察下列各式2×$\sqrt{\frac{2}{3}}$=$\sqrt{2+\frac{2}{3}}$
3×$\sqrt{\frac{3}{8}}$=$\sqrt{3+\frac{3}{8}}$
4×$\sqrt{\frac{4}{15}}$=$\sqrt{4+\frac{4}{15}}$
则依次第四个式子是5×$\sqrt{\frac{5}{24}}$=$\sqrt{5+\frac{5}{24}}$.用n(n>1)表示你观察得到的规律是n×$\sqrt{\frac{n}{{n}^{2}-1}}$=$\sqrt{n+\frac{n}{{n}^{2}-1}}$.
分析 第四个式子的整数为5,分数的分子与整数相同,分母是分子的平方减1,写出即可;
根据分数的分子与整数相同,分母是分子的平方减1解答.
解答 解:第四个式子为:5×$\sqrt{\frac{5}{24}}$=$\sqrt{5+\frac{5}{24}}$;
n×$\sqrt{\frac{n}{{n}^{2}-1}}$=$\sqrt{n+\frac{n}{{n}^{2}-1}}$.
故答案为:5×$\sqrt{\frac{5}{24}}$=$\sqrt{5+\frac{5}{24}}$;n×$\sqrt{\frac{n}{{n}^{2}-1}}$=$\sqrt{n+\frac{n}{{n}^{2}-1}}$.
点评 本题考查了二次根式的性质与化简,观察出分数的分子、分母与整数的关系是解题的关键.

练习册系列答案
相关题目
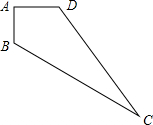 如图所示,在四边形ABCD中,∠A=90°,AB=3,AD=4,BC=13,CD=12.试求四边形ABCD的面积.
如图所示,在四边形ABCD中,∠A=90°,AB=3,AD=4,BC=13,CD=12.试求四边形ABCD的面积.
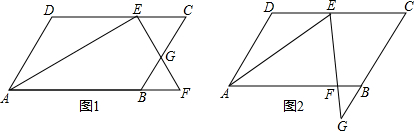
 在梯形ABCD中,AB∥CD,AC、BD交于点E,AD、BC的延长线交于点H,过点E作FG∥AB交AD于点F,交BC于点G,求证:AG、BF、EH三线共点.
在梯形ABCD中,AB∥CD,AC、BD交于点E,AD、BC的延长线交于点H,过点E作FG∥AB交AD于点F,交BC于点G,求证:AG、BF、EH三线共点.
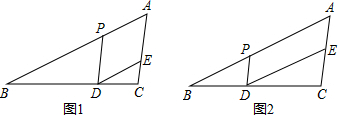
 如图,在△ABC中,AD⊥BC,CE⊥AB,垂足分别为点D、E.若BE=2AE,AD=3,tan∠BCE=$\frac{\sqrt{3}}{3}$,则CE=4.
如图,在△ABC中,AD⊥BC,CE⊥AB,垂足分别为点D、E.若BE=2AE,AD=3,tan∠BCE=$\frac{\sqrt{3}}{3}$,则CE=4.