题目内容
3.在一次数学课上,李老师对大家说:“你任意想一个非零数,然后按下列步骤操作,我会直接说出你运算的最后结果.”操作步骤如下:
第一步:计算这个数与1的和的平方,减去这个数与1的差的平方;
第二步:把第一步得到的数乘以25;
第三步:把第二步得到的数除以你想的这个数.
(1)若小明同学心里想的是数9,请帮他计算出最后结果:
(2)老师说:“同学们,无论你们心里想的是什么非零数,按照以上步骤进行操作,得到的最后结果都相等.”小明同学想验证这个结论,于是,设心里想的数是a(a≠0),请你帮小明完成这个验证过程.
分析 (1)根据每步的运算,找出运算结果,此题得解;
(2)根据三步操作可得出算式[(a+1)2-(a-1)2]×25÷a,展开化简后即可证出结论.
解答 解:(1)第一步:(9+1)2-(9-1)2=36;
第二步:25×36=900;
第三步:900÷9=100.
∴小明计算出最后结果为100.
(2)根据题意得:[(a+1)2-(a-1)2]×25÷a,
=(a+1+a-1)(a+1-a+1)×25÷a,
=4a×25÷a,
=100.
∴结论成立.
点评 本题考查了整式的混合运算以及列代数式,解题的关键是:(1)根据运算步骤列出算式;(2)根据运算步骤列出代数式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12. 已知,直线y=-$\sqrt{3}$x+$\sqrt{3}$与x轴、y轴分别交于点A、B,以线段AB为直角边在第一象限内作等腰三角形Rt△ABC,∠BAC=90°,且点P(1,a)为坐标系中一个动点.要使得△ABC和△ABP的面积相等,则实数a的值( )
已知,直线y=-$\sqrt{3}$x+$\sqrt{3}$与x轴、y轴分别交于点A、B,以线段AB为直角边在第一象限内作等腰三角形Rt△ABC,∠BAC=90°,且点P(1,a)为坐标系中一个动点.要使得△ABC和△ABP的面积相等,则实数a的值( )
 已知,直线y=-$\sqrt{3}$x+$\sqrt{3}$与x轴、y轴分别交于点A、B,以线段AB为直角边在第一象限内作等腰三角形Rt△ABC,∠BAC=90°,且点P(1,a)为坐标系中一个动点.要使得△ABC和△ABP的面积相等,则实数a的值( )
已知,直线y=-$\sqrt{3}$x+$\sqrt{3}$与x轴、y轴分别交于点A、B,以线段AB为直角边在第一象限内作等腰三角形Rt△ABC,∠BAC=90°,且点P(1,a)为坐标系中一个动点.要使得△ABC和△ABP的面积相等,则实数a的值( )| A. | a=4 | B. | a=±4 | C. | a=-3 | D. | a=±3 |
13.小明早晨上学时,每小时走5千米,中午放学沿原路回家时,每小时走4千米,结果回家所用的时间比上学所用的时间多10分钟,问小明家离学校有多远?设小明家离学校有x千米,那么所列方程是( )
| A. | $\frac{x}{5}$=$\frac{x}{4}$-10 | B. | $\frac{x}{5}$+$\frac{1}{6}$=$\frac{x}{4}$ | C. | 5x=4x+10 | D. | $\frac{x}{5}$-$\frac{x}{4}$=$\frac{1}{6}$ |
 在梯形ABCD中,AB∥CD,AC、BD交于点E,AD、BC的延长线交于点H,过点E作FG∥AB交AD于点F,交BC于点G,求证:AG、BF、EH三线共点.
在梯形ABCD中,AB∥CD,AC、BD交于点E,AD、BC的延长线交于点H,过点E作FG∥AB交AD于点F,交BC于点G,求证:AG、BF、EH三线共点.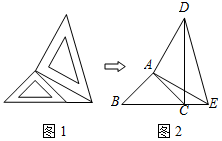 两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B,C,E在同一条直线上,连结DC.
两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B,C,E在同一条直线上,连结DC.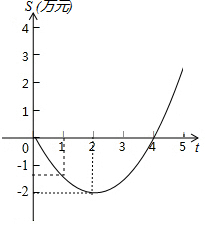 某电脑公司开发出一种软件,从研发到年初上市后,经历了从亏损到盈利的过程,如图中的图象是抛物线的一段,它刻画了该软件上市以来累积利润S(万元)与销售时间t(月)之间的函数关系(即前t个月的利润总和S与t之间的函数关系),根据图象提供的信息,解答下列问题:
某电脑公司开发出一种软件,从研发到年初上市后,经历了从亏损到盈利的过程,如图中的图象是抛物线的一段,它刻画了该软件上市以来累积利润S(万元)与销售时间t(月)之间的函数关系(即前t个月的利润总和S与t之间的函数关系),根据图象提供的信息,解答下列问题: 如图,在△ABC中,AD⊥BC,CE⊥AB,垂足分别为点D、E.若BE=2AE,AD=3,tan∠BCE=$\frac{\sqrt{3}}{3}$,则CE=4.
如图,在△ABC中,AD⊥BC,CE⊥AB,垂足分别为点D、E.若BE=2AE,AD=3,tan∠BCE=$\frac{\sqrt{3}}{3}$,则CE=4.