Question

9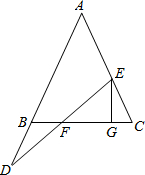．如图，在△ABC中，AB=AC，点E在线段AC上，D在AB的延长线上，连接DE交BC于F，过E作EG⊥BC于G．
（1）下列两个关系式：①DB=EC，②DF=EF，请你选择一个做为条件，另一个做为结论构成一个正确的命题，并给予证明．
你选择的条件是①，结论是②．（只需填序号）
（2）在（1）的条件下，求证：FG=$\frac{1}{2}$BC．

Answer 1

分析 （1）条件是①DB=EC，结论是②DF=EF．（也可以填条件是②，结论是①）．只要证明△FBD≌△FHE，即可解决问题．
（2）由（1）可知，EH=EC，EG⊥HC，推出GH=GC，由△BFD≌△FHE，推出BF=FH，即可推出FG=FH+HG=$\frac{1}{2}$BH+$\frac{1}{2}$HC=$\frac{1}{2}$（BH+HC）=$\frac{1}{2}$BC．

解答 （1）解：条件是①DB=EC，结论是②DF=EF．（也可以填条件是②，结论是①）．
理由：如图作，EH∥AD交BC于H．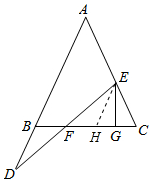

∵EH∥AD，
∴∠ABC=∠EHC，∠D=∠HEF，
∵AB=AC，
∴∠ABC=∠C=∠EHC，
∴EH=EC=BD，
在△FBD和△FEH中，
$\left\{\begin{array}{l}{∠D=∠HEF}\\{∠DFB=∠EFH}\\{BD=EH}\end{array}\right.$，
∴△FBD≌△FHE，
∴DF=EF．

（2）证明：由（1）可知，EH=EC，EG⊥HC，
∴GH=GC，
∵△BFD≌△FHE，
∴BF=FH，
∴FG=FH+HG=$\frac{1}{2}$BH+$\frac{1}{2}$HC=$\frac{1}{2}$（BH+HC）=$\frac{1}{2}$BC．

点评 本题考查全等三角形的判定和性质、等腰三角形的性质和判定等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，属于中考常考题型．