题目内容
4．计算：（1）$\sqrt{8}$÷$\sqrt{2}$=2；（2）$\sqrt{6{a}^{3}b}$÷$\sqrt{2ab}$=$\sqrt{3}$a；（3）$\frac{\sqrt{5}}{\sqrt{3}}$═$\frac{\sqrt{15}}{3}$；（4）1÷$\sqrt{3}$×$\frac{1}{\sqrt{3}}$=$\frac{1}{3}$．
分析 原式利用二次根式乘除法则，以及分母有理化法则计算即可得到结果．
解答 解：（1）原式=$\sqrt{8÷2}$=$\sqrt{4}$=2；
（2）原式=$\sqrt{6{a}^{3}b÷2ab}$=$\sqrt{3{a}^{2}}$=$\sqrt{3}$a；
（3）原式=$\frac{\sqrt{5}×\sqrt{3}}{\sqrt{3}×\sqrt{3}}$=$\frac{\sqrt{15}}{3}$；
（4）原式=$\frac{1}{\sqrt{3}}$×$\frac{1}{\sqrt{3}}$=$\frac{1}{3}$，
故答案为：（1）2；（2）$\sqrt{3}$a；（3）$\frac{\sqrt{15}}{3}$；（4）$\frac{1}{3}$
点评 此题考查了分母有理化，以及二次根式的乘除法，熟练掌握二次根式乘除法则及分母有理化法则是解本题的关键．
练习册系列答案
怎样学好牛津英语系列答案
导学教程高中新课标系列答案
相关题目
14．
如图，在四边形ABCD中，AD∥BC，AC，BD交于点O，过点O作EF∥AD交AB于点E，F，若AE=2，BE=5，OD=3，则BD长为（ ）
如图，在四边形ABCD中，AD∥BC，AC，BD交于点O，过点O作EF∥AD交AB于点E，F，若AE=2，BE=5，OD=3，则BD长为（ ）| A． | 6 | B． | $\frac{15}{2}$ | C． | $\frac{21}{2}$ | D． | $\frac{10}{3}$ |
12．
如图，⊙O的直径AB=10，CD是⊙O的弦，CD⊥AB，垂足为M，若OM：OB=3：5，则CD的长为（ ）
如图，⊙O的直径AB=10，CD是⊙O的弦，CD⊥AB，垂足为M，若OM：OB=3：5，则CD的长为（ ）| A． | 8 | B． | 6 | C． | 4 | D． | $\sqrt{91}$ |
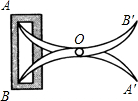如图，将两根钢条AA′，BB′的中点O钉在一起，使AA′，BB′能绕点O自由转动，就做成一个测量工具，测A′B′的长即等于内槽宽AB，这种测量方法的依据是两边和它们的夹角分别相等的两个三角形全等，全等三角形的对应边相等．．
如图，点E、F、C、B在同一直线上，AB=DE，∠B=∠E，要判定△ABC≌△DEF，还需要添加一个条件，你添加的条件是EF=BC（或EC=BF或∠D=∠A或∠EFD=∠BCA 或∠DFB=∠ACE或DF∥AC）．（写出一个即可）