题目内容
9.分解因式:a2+4b2+c4-4ab-2ac2+4bc2-1.分析 先分组得到原式=(a2+4b2-4ab)+(-2ac2+4bc2)+(c4-1),再根据完全平方公式,提取公因式法,平方差公式得到原式=(2b-a)2+2c2(2b-a)+(c2+1)(c2-1),再根据十字相乘法即可求解.
解答 解:a2+4b2+c4-4ab-2ac2+4bc2-1
=(a2+4b2-4ab)+(-2ac2+4bc2)+(c4-1)
=(2b-a)2+2c2(2b-a)+(c2+1)(c2-1)
=(2b-a+c2+1)(2b-a+c2-1).
点评 本题考查了因式分解-分组分解法,本题关键是式子分组,以及熟练掌握完全平方公式,提取公因式法,平方差公式,十字相乘法的计算方法.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
19.下列说法正确的是( )
| A. | 垂线段就是垂直于已知直线的线段 | |
| B. | 垂线段就是垂直于已知直线并且与已知直线相交的线段 | |
| C. | 垂线段是一条竖起来的线段 | |
| D. | 过直线外一点向该直线作垂线,这一点到垂足之间的线段叫垂线段 |
 如图,AB是⊙O的直径,且AB=10,弦MN的长为8,若弦MN的两端在圆周上滑动,始终与AB相交.记点A,B到MN的距离为h1,h2.则|h1-h2|等于( )
如图,AB是⊙O的直径,且AB=10,弦MN的长为8,若弦MN的两端在圆周上滑动,始终与AB相交.记点A,B到MN的距离为h1,h2.则|h1-h2|等于( ) 已知:如图,△ABC中,D、E分别是边BC、AB的中点,AD、CE相交于G,请写出GE:CE的比值,并加以证明.
已知:如图,△ABC中,D、E分别是边BC、AB的中点,AD、CE相交于G,请写出GE:CE的比值,并加以证明.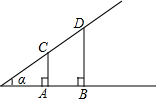 如图,A,B,C,D分别是∠α边上的四个点,且CA,DB均垂直于∠α的一条边,如果CA=AB=2,BD=3,那么tanα=$\frac{1}{2}$.
如图,A,B,C,D分别是∠α边上的四个点,且CA,DB均垂直于∠α的一条边,如果CA=AB=2,BD=3,那么tanα=$\frac{1}{2}$.