题目内容
19.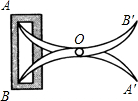 如图,将两根钢条AA′,BB′的中点O钉在一起,使AA′,BB′能绕点O自由转动,就做成一个测量工具,测A′B′的长即等于内槽宽AB,这种测量方法的依据是两边和它们的夹角分别相等的两个三角形全等,全等三角形的对应边相等..
如图,将两根钢条AA′,BB′的中点O钉在一起,使AA′,BB′能绕点O自由转动,就做成一个测量工具,测A′B′的长即等于内槽宽AB,这种测量方法的依据是两边和它们的夹角分别相等的两个三角形全等,全等三角形的对应边相等..
分析 由O是AA′、BB′的中点,可得AO=A′O,BO=B′O,再有∠AOA′=∠BOB′,可以根据全等三角形的判定方法SAS,判定△OAB≌△OA′B′,根据全等三角形的性质即可得到结论.
解答 解:∵O是AA′、BB′的中点,
∴AO=A′O,BO=B′O,
在△OAB和△OA′B′中$\left\{\begin{array}{l}{AO=A′O}\\{∠AOA′=∠BOB′}\\{BO=B′O}\end{array}\right.$,
∴△OAB≌△OA′B′(SAS),
∴AB=A′B′,
故两边和它们的夹角分别相等的两个三角形全等,全等三角形的对应边相等.
故答案为:两边和它们的夹角分别相等的两个三角形全等,全等三角形的对应边相等.
点评 此题主要全等三角形的应用,关键是掌握全等三角形的判定方法:SSS、SAS、ASA、AAS,HL,要证明两个三角形全等,必须有对应边相等这一条件.

练习册系列答案
相关题目
9.半径为2的圆内有两条互相垂直的弦AB和CD,它们的交点E到圆心O的距离等于1,则AB2+CD2=( )
| A. | 28 | B. | 26 | C. | 18 | D. | 35 |
7.甲、乙两名工人同时加工同一种零件,现根据两人7天产品中每天出现的次品数情况制成如下统计表,依据相关信息,解答下列问题:
(1)在统计表中,工人甲7天出现次品数的众数为2,其极差是4,工人乙7天出现次品数的中位数为1;
(2)根据题目所给数据,通过计算判断甲、乙两名工人谁出现次品的波动要小些;
(3)请估计甲、乙加工该种零件30天共出现次品多少件?
| 第1天 | 第2天 | 第3天 | 第4天 | 第5天 | 第6天 | 第7天 | |
| 甲(件) | 2 | 2 | 0 | 3 | 1 | 2 | 4 |
| 乙(件) | 1 | 0 | 2 | 1 | 1 | 0 | 2 |
(2)根据题目所给数据,通过计算判断甲、乙两名工人谁出现次品的波动要小些;
(3)请估计甲、乙加工该种零件30天共出现次品多少件?
 将长方形ABCD沿EF折叠,得到如图所示的图形,已知∠BEF=50°,则∠AEB′的大小是80度.
将长方形ABCD沿EF折叠,得到如图所示的图形,已知∠BEF=50°,则∠AEB′的大小是80度.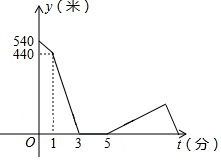 “欢乐跑中国•重庆站”比赛前夕,小刚和小强相约晨练跑步.小刚比小强早1分钟跑步出门,3分钟后他们相遇.两人寒暄2分钟后,决定进行跑步比赛.比赛时小刚的速度始终是180米/分,小强的速度是220米/分.比赛开始10分钟后,因雾霾严重,小强突感身体不适,于是他按原路以出门时的速度返回,直到他们再次相遇.如图所示是小刚、小强之间的距离y(千米)与小刚跑步所用时间x(分钟)之间的函数图象.问小刚从家出发到他们再次相遇时,一共用了$\frac{49}{3}$分钟.
“欢乐跑中国•重庆站”比赛前夕,小刚和小强相约晨练跑步.小刚比小强早1分钟跑步出门,3分钟后他们相遇.两人寒暄2分钟后,决定进行跑步比赛.比赛时小刚的速度始终是180米/分,小强的速度是220米/分.比赛开始10分钟后,因雾霾严重,小强突感身体不适,于是他按原路以出门时的速度返回,直到他们再次相遇.如图所示是小刚、小强之间的距离y(千米)与小刚跑步所用时间x(分钟)之间的函数图象.问小刚从家出发到他们再次相遇时,一共用了$\frac{49}{3}$分钟.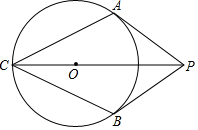 已知:如图,PA,PB是⊙O的切线,切点分别为A,B,连结PO并延长,交⊙O于点C,求证:AC=BC.
已知:如图,PA,PB是⊙O的切线,切点分别为A,B,连结PO并延长,交⊙O于点C,求证:AC=BC.