题目内容
14. 如图,在四边形ABCD中,AD∥BC,AC,BD交于点O,过点O作EF∥AD交AB于点E,F,若AE=2,BE=5,OD=3,则BD长为( )
如图,在四边形ABCD中,AD∥BC,AC,BD交于点O,过点O作EF∥AD交AB于点E,F,若AE=2,BE=5,OD=3,则BD长为( )| A. | 6 | B. | $\frac{15}{2}$ | C. | $\frac{21}{2}$ | D. | $\frac{10}{3}$ |
分析 根据平行线分线段成比例的性质解答即可.
解答 解:∵AD∥BC,EF∥AD,
∴EF∥BC,
∴$\frac{AE}{BE}=\frac{AO}{OC}=\frac{2}{5}$,$\frac{OA}{OC}=\frac{OD}{OB}$,
∵OD=3,
∴$\frac{2}{5}=\frac{3}{OB}$,解得:OB=$\frac{15}{2}$,
∴BD=OD+OB=$\frac{15}{2}+3=\frac{21}{2}$,
故选C
点评 本题主要考查平行线分线段成比例,掌握平行线所分线段对应成比例是解题的关键.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
9.半径为2的圆内有两条互相垂直的弦AB和CD,它们的交点E到圆心O的距离等于1,则AB2+CD2=( )
| A. | 28 | B. | 26 | C. | 18 | D. | 35 |
6. 如图,在△ABC中,∠ACB=90°,∠ABC=60°,BD平分∠ABC,P点是BD的中点,若AD=8,则CP的长为( )
如图,在△ABC中,∠ACB=90°,∠ABC=60°,BD平分∠ABC,P点是BD的中点,若AD=8,则CP的长为( )
 如图,在△ABC中,∠ACB=90°,∠ABC=60°,BD平分∠ABC,P点是BD的中点,若AD=8,则CP的长为( )
如图,在△ABC中,∠ACB=90°,∠ABC=60°,BD平分∠ABC,P点是BD的中点,若AD=8,则CP的长为( )| A. | 3 | B. | 3.5 | C. | 4 | D. | 4.5 |

 如图,AB是⊙O的直径,且AB=10,弦MN的长为8,若弦MN的两端在圆周上滑动,始终与AB相交.记点A,B到MN的距离为h1,h2.则|h1-h2|等于( )
如图,AB是⊙O的直径,且AB=10,弦MN的长为8,若弦MN的两端在圆周上滑动,始终与AB相交.记点A,B到MN的距离为h1,h2.则|h1-h2|等于( )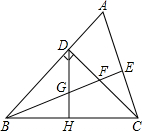 如图,在△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,BE与CD相交于点F,BF=2CE,H是BC边的中点,连接DH与BE相交于点G.下列结论中:①∠A=67.5°;②DF=AD;③BE=2BG;④DH⊥BC,正确的个数是( )
如图,在△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,BE与CD相交于点F,BF=2CE,H是BC边的中点,连接DH与BE相交于点G.下列结论中:①∠A=67.5°;②DF=AD;③BE=2BG;④DH⊥BC,正确的个数是( )