题目内容
12．
如图，⊙O的直径AB=10，CD是⊙O的弦，CD⊥AB，垂足为M，若OM：OB=3：5，则CD的长为（ ）| A． | 8 | B． | 6 | C． | 4 | D． | $\sqrt{91}$ |
分析 直接利用垂径定理得出MC=DM，再利用勾股定理得出CM的长，进而得出出DC的长．
解答 
解：连接CO，
∵⊙O的直径AB=10，
∴BO=CO=5，
∵OM：OB=3：5，
∴OM=3，
∴在直角三角形COM中，
MC=$\sqrt{C{O}^{2}-M{O}^{2}}$=4，
∵CD⊥AB，
∴MC=MD=4，
∴DC=8．
故选：A．
点评 此题主要考查了垂径定理以及勾股定理，正确得出MC的长是解题关键．
练习册系列答案
字词句段篇系列答案
相关题目
3．
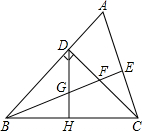如图，在△ABC中，∠ABC=45°，CD⊥AB于D，BE平分∠ABC，且BE⊥AC于E，BE与CD相交于点F，BF=2CE，H是BC边的中点，连接DH与BE相交于点G．下列结论中：①∠A=67.5°；②DF=AD；③BE=2BG；④DH⊥BC，正确的个数是（ ）
如图，在△ABC中，∠ABC=45°，CD⊥AB于D，BE平分∠ABC，且BE⊥AC于E，BE与CD相交于点F，BF=2CE，H是BC边的中点，连接DH与BE相交于点G．下列结论中：①∠A=67.5°；②DF=AD；③BE=2BG；④DH⊥BC，正确的个数是（ ）| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
已知：如图，△ABC中，D、E分别是边BC、AB的中点，AD、CE相交于G，请写出GE：CE的比值，并加以证明．
7．甲、乙两名工人同时加工同一种零件，现根据两人7天产品中每天出现的次品数情况制成如下统计表，依据相关信息，解答下列问题：
（1）在统计表中，工人甲7天出现次品数的众数为2，其极差是4，工人乙7天出现次品数的中位数为1；
（2）根据题目所给数据，通过计算判断甲、乙两名工人谁出现次品的波动要小些；
（3）请估计甲、乙加工该种零件30天共出现次品多少件？
| 第1天 | 第2天 | 第3天 | 第4天 | 第5天 | 第6天 | 第7天 | |
| 甲（件） | 2 | 2 | 0 | 3 | 1 | 2 | 4 |
| 乙（件） | 1 | 0 | 2 | 1 | 1 | 0 | 2 |
（2）根据题目所给数据，通过计算判断甲、乙两名工人谁出现次品的波动要小些；
（3）请估计甲、乙加工该种零件30天共出现次品多少件？