题目内容
8.(1)计算:$(3\sqrt{12}-2\sqrt{\frac{1}{3}}+\sqrt{48})÷2\sqrt{3}$(2)先化简,再求值:$\frac{2}{a-1}+\frac{{{a^2}-4a+4}}{{{a^2}-1}}÷\frac{a-2}{a+1}$,其中$a=1+\sqrt{2}$.
分析 (1)根据二次根式混合运算顺序先化简根式,再合并括号内的同类二次根式,最后相除可得;
(2)先将各分式分子分母因式分解、除法转化为乘法,再约分后即为同分母分式相加,将a的值代入,分母有理化可得.
解答 解:(1)原式=(6$\sqrt{3}$-$\frac{2\sqrt{3}}{3}$+4$\sqrt{3}$)$÷2\sqrt{3}$
=$\frac{28\sqrt{3}}{3}$$÷2\sqrt{3}$
=$\frac{14}{3}$;
(2)原式=$\frac{2}{a-1}+\frac{(a-2)^{2}}{(a+1)(a-1)}$•$\frac{a+1}{a-2}$
=$\frac{2}{a-1}$+$\frac{a-2}{a-1}$
=$\frac{a}{a-1}$,
当a=1+$\sqrt{2}$时,
原式=$\frac{1+\sqrt{2}}{1+\sqrt{2}-1}$
=$\frac{1+\sqrt{2}}{\sqrt{2}}$
=$\frac{2+\sqrt{2}}{2}$.
点评 本题主要考查二次根式的混合运算及分式的化简求值能力,熟练掌握这些基本运算的计算步骤是解题的根本也是关键.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案
相关题目
19.如果菱形的边长是α,一个内角是60度,那么菱形较短的对角线长等于( )
| A. | $\frac{1}{2}α$ | B. | $\frac{{\sqrt{3}}}{2}a$ | C. | a | D. | $\sqrt{3a}$ |
16.下列计算正确的是( )
| A. | (4x+5y)2=16x2+20xy+25y2 | B. | (-2x3y4z)3=-8x9y12z3 | ||
| C. | (a-b)(a+b)=2a-2b | D. | (-a6)÷(-a)4=a2 |
3.为确保信息安全,信息需加密传输,发送方由明文→密文(加密);接收方由密文→明文(解密).已知加密规则为:明文a,b,c,d对应密文a+2b,2b+c,2c+3d,4d.例如:明文1,2,3,4对应的密文5,7,18,16.当接收方收到密文14,9,23,28时,则解密得到的明文为( )
| A. | 4,6,1,7 | B. | 4,1,6,7 | C. | 6,4,1,7 | D. | 1,6,4,7 |
17. 如图,Rt△ABC中,∠C=90°,AC=6,BC=8,AD平分∠BAC,则点B到AD的距离是( )
如图,Rt△ABC中,∠C=90°,AC=6,BC=8,AD平分∠BAC,则点B到AD的距离是( )
 如图,Rt△ABC中,∠C=90°,AC=6,BC=8,AD平分∠BAC,则点B到AD的距离是( )
如图,Rt△ABC中,∠C=90°,AC=6,BC=8,AD平分∠BAC,则点B到AD的距离是( )| A. | 3 | B. | 4 | C. | 2$\sqrt{5}$ | D. | $\frac{{12\sqrt{13}}}{13}$ |
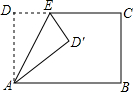 将长方形ABCD沿AE折叠,得到如图所示的图形,若∠CED′=50°,则∠EAB的大小是65°.
将长方形ABCD沿AE折叠,得到如图所示的图形,若∠CED′=50°,则∠EAB的大小是65°.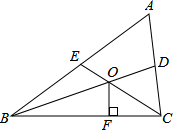 如图,△ABC 的中线BD、CE相交于点O,OF⊥BC,且AB=6,BC=5,AC=4,OF=3,则四边形ADOE的面积是7.5.
如图,△ABC 的中线BD、CE相交于点O,OF⊥BC,且AB=6,BC=5,AC=4,OF=3,则四边形ADOE的面积是7.5.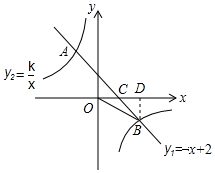 如图,一次函数y1=-x+2的图象与反比例函数y2=$\frac{k}{x}$的图象交于A,B两点,与x轴交于点C,已知tan∠BOC=$\frac{1}{2}$.
如图,一次函数y1=-x+2的图象与反比例函数y2=$\frac{k}{x}$的图象交于A,B两点,与x轴交于点C,已知tan∠BOC=$\frac{1}{2}$.