如图.△ABC 的中线BD.CE相交于点O.OF⊥BC.且AB=6.BC=5.AC=4.OF=3.则四边形ADOE的面积是7.5．题目和参考答案——青夏教育精英家教网——

题目内容

20．

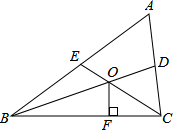如图，△ABC 的中线BD、CE相交于点O，OF⊥BC，且AB=6，BC=5，AC=4，OF=3，则四边形ADOE的面积是7.5．

分析首先根据三角形的面积=底×高÷2，求出△BOC的面积是多少；然后根据三角形的中线将三角形分成面积相等的两部分，可得△BCD、△ACE的面积均是△ABC的面积的一半，据此判断出四边形ADOE的面积等于△BOC的面积，据此解答即可．

解答解：∵BD、CE均是△ABC的中线，
∴S_△BCD=S_△ACE=$\frac{1}{2}$S_△ABC，
∴S_{四边形ADOE}+S_△COD=S_△BOC+S_△COD，
∴S_{四边形ADOE}=S_△BOC=5×3÷2=7.5．
故答案为：7.5．

点评此题主要考查了三角形的面积的求法，以及三角形的中线的性质，要熟练掌握，解答此题的关键要明确：（1）三角形的中线将三角形分成面积相等的两部分；（2）三角形的面积=底×高÷2．

练习册系列答案

步步高高考总复习系列答案

全能测控期末小状元系列答案

暑假作业西南大学出版社系列答案

大赢家期末真题卷系列答案

快乐假期暑假作业新蕾出版社系列答案

步步高练加测系列答案

汇练系列答案

快乐假期暑假作业新疆人民出版社系列答案

激活思维标准期末考卷100分系列答案

智趣暑假温故知新系列答案

相关题目

10．计算：
（1）2$\sqrt{\frac{1}{2}}$-6$\sqrt{\frac{1}{3}}$+$\sqrt{8}$
（2）2$\sqrt{10}$×$3\sqrt{5}$-4$\sqrt{2}$
（3）（3$\sqrt{48}$-2$\sqrt{27}$）$÷\sqrt{3}$
（4）$\sqrt{1\frac{2}{3}}÷\sqrt{2\frac{1}{3}}×\sqrt{1\frac{2}{5}}$．

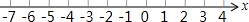解不等式组：$\left\{\begin{array}{l}{2x＞3x-2}\\{\frac{2x-1}{3}≥\frac{1}{2}x-\frac{2}{3}}\end{array}\right.$，并把解集在数轴上表示出来．

8．（1）计算：$（3\sqrt{12}-2\sqrt{\frac{1}{3}}+\sqrt{48}）÷2\sqrt{3}$
（2）先化简，再求值：$\frac{2}{a-1}+\frac{{{a^2}-4a+4}}{{{a^2}-1}}÷\frac{a-2}{a+1}$，其中$a=1+\sqrt{2}$．

15．人造地球卫星要绕地球旋转，必须克服地球引力，克服地球引力的速度称为逃逸速度，逃逸速度的计算公式为$v=\sqrt{gR}$（千米/秒），其中g=0.0098千米/秒²，R=6370千米，求逃逸速度．（结果保留2个有效数字）

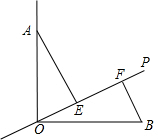如图，∠AOB=90°，OA=OB，OP是∠AOB内可以绕着点O自由转动的一条射线，分别过点A、B作AE⊥OP、BF⊥OP，垂足分别为点E、F，假设OP从OB出发，绕着点O逆时针转动到OA（OP不与OB、OA重合），转动的角度为α．
（1）当0°＜α＜45°时，线段AE、BF、EF的长度有怎样的数量关系？为什么？
（2）当45°＜α＜90°时，线段AE、BF、EF的长度又有怎样的数量关系？为什么？

12．已知线段AB∥CD，直线EF∥AB，若点P在直线EF上，连接PA、PC．
（1）如图1，直线EF在线段AB、CD之间，点P在中间位置时，写出∠A、∠C、∠APC三个角之间的数量关系，并证明你的结论；
（2）如图2，直线EF在线段AB、CD之间，点P在偏左位置时，写出∠A、∠C、∠APC三个角之间的数量关系，并证明你的结论；
（3）如图3，直线EF在线段AB上方，点P在偏左位置时，写出∠PAB、∠PCD、∠APC三个角之间的数量关系，并证明你的结论．

9．如果一个三角形的三边长为5、12、13，与其相似的三角形的最长的边长为39，那么较大的三角形的面积为（　　）

10．当k分别取0，1时，函数y=（1-k）x²-4x+5-k都有最小值吗？写出你的判断，并说明理由．