题目内容
18.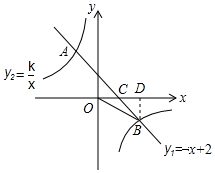 如图,一次函数y1=-x+2的图象与反比例函数y2=$\frac{k}{x}$的图象交于A,B两点,与x轴交于点C,已知tan∠BOC=$\frac{1}{2}$.
如图,一次函数y1=-x+2的图象与反比例函数y2=$\frac{k}{x}$的图象交于A,B两点,与x轴交于点C,已知tan∠BOC=$\frac{1}{2}$.(1)求反比例函数的解析式.
(2)当y1=y2时,求x的取值范围.
分析 (1)根据已知得出OD=2BD,设B(-2m,m),代入y1=-x+2,求出B的坐标,代入y2=$\frac{k}{x}$,根据待定系数法求出即可;
(2)联立方程,解方程即可求得.
解答 解:(1)∵tan∠BOC=$\frac{1}{2}$,
∴OD=2BD,
∴设B(-2m,m),
代入y1=-x+2得m=2m+2,
解得m=-2,
∴B(4,-2),
∴k=-2×4=-8,
∴反比例函数的解析式为y=-$\frac{8}{x}$;
(2)解-$\frac{8}{x}$=-x+2得x=-2或x=4,
故当y1=y2时,x的取值为-2或4.
点评 本题考查了一次函数和反比例函数的交点问题,用待定系数法反比例函数的解析式的应用,主要考查学生的计算能力,题目比较好,难度适中.

练习册系列答案
相关题目
9.如果一个三角形的三边长为5、12、13,与其相似的三角形的最长的边长为39,那么较大的三角形的面积为( )
| A. | 90 | B. | 180 | C. | 270 | D. | 540 |
13.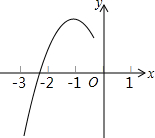 已知抛物线y=ax2+bx+c的顶点为D(-1,3),与x轴的一个交点在(-3,0)和(-2,0)之间,其部分图象如图,则以下结论:
已知抛物线y=ax2+bx+c的顶点为D(-1,3),与x轴的一个交点在(-3,0)和(-2,0)之间,其部分图象如图,则以下结论:
①b2-4ac>0;②c-a=3;③a+b+c<0;④方程ax2+bx+c=m(m≥2)一定有实数根,其中正确的结论为( )
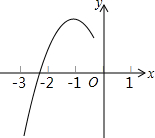 已知抛物线y=ax2+bx+c的顶点为D(-1,3),与x轴的一个交点在(-3,0)和(-2,0)之间,其部分图象如图,则以下结论:
已知抛物线y=ax2+bx+c的顶点为D(-1,3),与x轴的一个交点在(-3,0)和(-2,0)之间,其部分图象如图,则以下结论:①b2-4ac>0;②c-a=3;③a+b+c<0;④方程ax2+bx+c=m(m≥2)一定有实数根,其中正确的结论为( )
| A. | ②③ | B. | ①③ | C. | ①②③ | D. | ①②④ |
3.已知关于x的不等式ax>b的解为x<3,那么下列关于x的不等式中解为x>3的是( )
| A. | -2ax>-2b | B. | 2ax>2b | C. | ax+2>b+2 | D. | ax-2>b-2 |
7.下列四个图形能围成棱柱的有几个( )
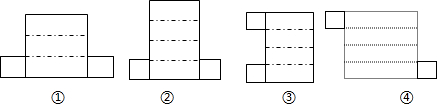

| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |