若$\frac{a}{2}$=$\frac{b}{3}$.则$\frac{a+b}{a}$的值为$\frac{5}{2}$．题目和参考答案——青夏教育精英家教网—

题目内容

13．若$\frac{a}{2}$=$\frac{b}{3}$，则$\frac{a+b}{a}$的值为$\frac{5}{2}$．

分析根据比例设a=2k，b=3k，然后代入比例式进行计算即可得解．

解答解：∵$\frac{a}{2}$=$\frac{b}{3}$，
∴设a=2k，b=3k，
∴$\frac{a+b}{a}$=$\frac{2k+3k}{2k}$=$\frac{5}{2}$．
故答案为：$\frac{5}{2}$．

点评本题考查了比例的性质，利用“设k法”求解更简便．

练习册系列答案

相关题目

3．以下列各组数为边长，能构成直角三角形的是（　　）

A．

1、2、3

B．

$\frac{1}{3}$，$\frac{1}{4}$，$\frac{1}{5}$

4．如果两个角的两边分别平行，而其中一个角比另一个角的4倍少30°，那么这两个角是（　　）

	A．	42°、138°		B．	都是10°
	C．	42°、138°或10°、10°		D．	以上都不对

1．

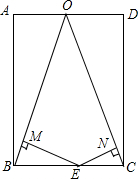如图，在矩形ABCD中，AB=3，BC=2，O是AD的中点，连接OB、OC，点E在线段BC上（点E不与点B、C重合），过点E作EM⊥OB于M，EN⊥OC于N，则EM+EN的值为（　　）

$\frac{3}{10}\sqrt{10}$

D．

$\frac{3}{5}\sqrt{10}$

8．（1）计算：$（3\sqrt{12}-2\sqrt{\frac{1}{3}}+\sqrt{48}）÷2\sqrt{3}$
（2）先化简，再求值：$\frac{2}{a-1}+\frac{{{a^2}-4a+4}}{{{a^2}-1}}÷\frac{a-2}{a+1}$，其中$a=1+\sqrt{2}$．

18．（1）探究发现：
下面是一道例题及其解答过程，请补充完整：
如图①在等边△ABC内部，有一点P，若∠APB=150°．求证：AP²+BP²=CP²
证明：将△APC绕A点逆时针旋转60°，得到△AP′B，连接PP′，则△APP′为等边三角形
∴∠APP′=60° PA=PP′PC=P′B
∵∠APB=150°∴∠BPP′=90°
∴P′P²+BP²=P′B²
即PA²+PB²=PC²
（2）类比延伸：
如图②在等腰三角形ABC中，∠BAC=90°，内部有一点P，若∠APB=135°，试判断线段PA、PB、PC之间的数量关系，并证明．
（3）联想拓展：
如图③在△ABC中，∠BAC=120°，AB=AC，点P在直线AB上方，且∠APB=60°，满足（kPA）²+PB²=PC²，请直接写出k的值．

5．

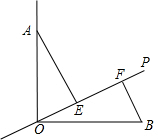如图，∠AOB=90°，OA=OB，OP是∠AOB内可以绕着点O自由转动的一条射线，分别过点A、B作AE⊥OP、BF⊥OP，垂足分别为点E、F，假设OP从OB出发，绕着点O逆时针转动到OA（OP不与OB、OA重合），转动的角度为α．
（1）当0°＜α＜45°时，线段AE、BF、EF的长度有怎样的数量关系？为什么？
（2）当45°＜α＜90°时，线段AE、BF、EF的长度又有怎样的数量关系？为什么？

2．一个正方体的体积是16cm³，另一正方体的体积是这个正方体体积的4倍，求另一个正方体的表面积．

3．已知关于x的不等式ax＞b的解为x＜3，那么下列关于x的不等式中解为x＞3的是（　　）

试题分类