题目内容

18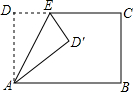．将长方形ABCD沿AE折叠，得到如图所示的图形，若∠CED′=50°，则∠EAB的大小是65°．

分析 首先由邻补角的定义求得∠DED′=130°，然后由翻折的性质可知：∠DEA=65°，由平行线的性质可求得∠EAB的度数．

解答 解：∵∠CED′=50°，
∴∠DED′=130°，
由翻折的性质可知：∠DEA=∠D′EA．
∴∠DEA=$\frac{1}{2}$∠DED′=$\frac{1}{2}$×130°=65°，
∵ABCD为矩形，
∴DC∥AB，
∴∠EAB=∠DEA=65°，
故答案为：65°．

点评 本题主要考查的是翻折变换、矩形的性质、邻补角的定义，求得∠DEA的度数是解题的关键．

练习册系列答案
相关题目
8．若等边△ABC的边长为4cm，那么△ABC的面积为（　　）
A．2$\sqrt{3}$cm2B．4$\sqrt{3}$cm2C．6$\sqrt{3}$cm2D．8cm2
9．2m=a，2n=b，则22m+3n=a2b3（用a、b的代数式表示）．
6．若关于x、y的方程组$\left\{\begin{array}{l}2x+y=k\\ x+2y=3\end{array}\right.$的解也是方程x+y=1的解，求k的值．
13．若4a2-2ka+9是一个完全平方的展开形式，则k的值为（　　）
A．6B．±6C．12D．±12
3．以下列各组数为边长，能构成直角三角形的是（　　）
A．1、2、3B．$\frac{1}{3}$，$\frac{1}{4}$，$\frac{1}{5}$C．0.3、0.4、0.5D．32、42、52
10．计算：
（1）2$\sqrt{\frac{1}{2}}$-6$\sqrt{\frac{1}{3}}$+$\sqrt{8}$
（2）2$\sqrt{10}$×$3\sqrt{5}$-4$\sqrt{2}$
（3）（3$\sqrt{48}$-2$\sqrt{27}$）$÷\sqrt{3}$
（4）$\sqrt{1\frac{2}{3}}÷\sqrt{2\frac{1}{3}}×\sqrt{1\frac{2}{5}}$．
7．解方程：
（1）2x-$\frac{2}{3}$（x+3）=-x+3        
（2）$\frac{3y-1}{4}-1=\frac{5y-7}{6}$．
8．（1）计算：$（3\sqrt{12}-2\sqrt{\frac{1}{3}}+\sqrt{48}）÷2\sqrt{3}$
（2）先化简，再求值：$\frac{2}{a-1}+\frac{{{a^2}-4a+4}}{{{a^2}-1}}÷\frac{a-2}{a+1}$，其中$a=1+\sqrt{2}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网