题目内容
19.如果菱形的边长是α,一个内角是60度,那么菱形较短的对角线长等于( )| A. | $\frac{1}{2}α$ | B. | $\frac{{\sqrt{3}}}{2}a$ | C. | a | D. | $\sqrt{3a}$ |
分析 由四边形ABCD是菱形,∠B=60°,可得△ABC是等边三角形,根据等边三角形的性质可求得菱形较短的对角线长等于菱形的边长.
解答 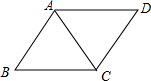 解:如图,∵四边形ABCD是菱形,
解:如图,∵四边形ABCD是菱形,
∴AB=BC=a,
∵∠B=60°,
∴△ABC是等边三角形,
∴AC=AB=BC=a.
即此菱形较短的对角线长是:a.
故选C.
点评 此题考查了菱形的性质以及等边三角形的判定与性质.此题难度不大,注意掌握数形结合思想的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.如果两个角的两边分别平行,而其中一个角比另一个角的4倍少30°,那么这两个角是( )
| A. | 42°、138° | B. | 都是10° | ||
| C. | 42°、138°或10°、10° | D. | 以上都不对 |
9.如果一个三角形的三边长为5、12、13,与其相似的三角形的最长的边长为39,那么较大的三角形的面积为( )
| A. | 90 | B. | 180 | C. | 270 | D. | 540 |
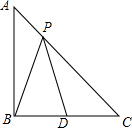 已知:如图,在等腰Rt△ABC中,∠ABC=90°,AB=2,D为BC的中点,P为线段AC上任意一点,则PB+PD的最小值为$\sqrt{5}$.
已知:如图,在等腰Rt△ABC中,∠ABC=90°,AB=2,D为BC的中点,P为线段AC上任意一点,则PB+PD的最小值为$\sqrt{5}$. 解不等式组:$\left\{\begin{array}{l}{2x>3x-2}\\{\frac{2x-1}{3}≥\frac{1}{2}x-\frac{2}{3}}\end{array}\right.$,并把解集在数轴上表示出来.
解不等式组:$\left\{\begin{array}{l}{2x>3x-2}\\{\frac{2x-1}{3}≥\frac{1}{2}x-\frac{2}{3}}\end{array}\right.$,并把解集在数轴上表示出来.