题目内容
17. 如图,Rt△ABC中,∠C=90°,AC=6,BC=8,AD平分∠BAC,则点B到AD的距离是( )
如图,Rt△ABC中,∠C=90°,AC=6,BC=8,AD平分∠BAC,则点B到AD的距离是( )| A. | 3 | B. | 4 | C. | 2$\sqrt{5}$ | D. | $\frac{{12\sqrt{13}}}{13}$ |
分析 过点D作DE⊥AB交AB于E,设CD=x,则BD=8-x,根据角平分线的性质得到$\frac{CD}{BD}=\frac{AC}{AB}$,求得CD=3,求得S△ABD=$\frac{1}{2}$AB•DE=$\frac{1}{2}×10×$3=15,由勾股定理得到AD=$\sqrt{A{C}^{2}+C{D}^{2}}$=3$\sqrt{5}$,根据三角形的面积公式即可得到结论.
解答  解:过点D作DE⊥AB交AB于E,
解:过点D作DE⊥AB交AB于E,
设CD=x,则BD=8-x,
∵AD平分∠BAC,
∴$\frac{CD}{BD}=\frac{AC}{AB}$,即$\frac{x}{8-x}=\frac{6}{10}$,
∴x=3,
∴CD=3,
∴S△ABD=$\frac{1}{2}$AB•DE=$\frac{1}{2}×10×$3=15,
∵AD=$\sqrt{A{C}^{2}+C{D}^{2}}$=3$\sqrt{5}$,
设BD到AD的距离是h,
∴S△ABD=$\frac{1}{2}$AD•h,
∴h=2$\sqrt{5}$.
故选C.
点评 本题考查了角平分线的性质,三角形的面积公式,三角形的角平分线定理,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
9.如果一个三角形的三边长为5、12、13,与其相似的三角形的最长的边长为39,那么较大的三角形的面积为( )
| A. | 90 | B. | 180 | C. | 270 | D. | 540 |
7.下列四个图形能围成棱柱的有几个( )
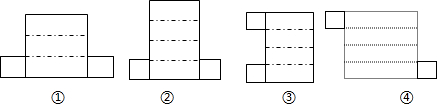

| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
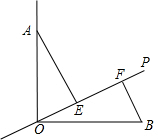 如图,∠AOB=90°,OA=OB,OP是∠AOB内可以绕着点O自由转动的一条射线,分别过点A、B作AE⊥OP、BF⊥OP,垂足分别为点E、F,假设OP从OB出发,绕着点O逆时针转动到OA(OP不与OB、OA重合),转动的角度为α.
如图,∠AOB=90°,OA=OB,OP是∠AOB内可以绕着点O自由转动的一条射线,分别过点A、B作AE⊥OP、BF⊥OP,垂足分别为点E、F,假设OP从OB出发,绕着点O逆时针转动到OA(OP不与OB、OA重合),转动的角度为α.