题目内容
4. 如图,在梯形ABCD中,AD∥BC,点P从点A出发沿AD向点D运动,同时点Q从点C出发沿CB向点B运动,已知点P的运动速度为1cm/s,点Q的运动速度为2cm/s,AD=4cm,BC=8cm,运动时间为t.
如图,在梯形ABCD中,AD∥BC,点P从点A出发沿AD向点D运动,同时点Q从点C出发沿CB向点B运动,已知点P的运动速度为1cm/s,点Q的运动速度为2cm/s,AD=4cm,BC=8cm,运动时间为t.(1)当t为何值时,四边形ABQD是平行四边形?
(2)当t为何值时,四边形ABQP是平行四边形?
分析 (1)若四边形ABQD是平行四边形,则AD=BQ,进而可得到关于t的方程,解方程求出t的值即可;
(2)若四边形ABQP是平行四边形,则AP=BQ,进而可得到关于t的方程,解方程求出t的值即可
解答 解:(1)∵AD∥BC,
∴若四边形ABQD是平行四边形,则AD=BQ,
∵已知点P的运动速度为1cm/s,点Q的运动速度为2cm/s,BC=8cm,
∴BQ=8-2t,
∵AD=4cm,
∴8-2t=4,
∴t=2;
(2))∵AD∥BC,
∴若四边形ABQP是平行四边形,则AP=BQ,
∵已知点P的运动速度为1cm/s,点Q的运动速度为2cm/s,BC=8cm,AD=4cm,
∴8-2t=t,
∴t=$\frac{8}{3}$.
点评 此题主要考查了梯形的性质以及平行四边形的判定,解题关键是掌握一组对边平行且相等的四边形是平行四边形.

练习册系列答案
相关题目
 如图,在△ABC中,∠C=90°,M为斜边AB上的一点,MN⊥AB交AC于N,若AM=3cm,AB:AC=5:3,求AN的长.
如图,在△ABC中,∠C=90°,M为斜边AB上的一点,MN⊥AB交AC于N,若AM=3cm,AB:AC=5:3,求AN的长. 如图,TQ切⊙O于点A,∠BAQ=60°,连接BO并延长与⊙O交于点C,与OA的延长线交于点T,若TC=2,求TA的长.
如图,TQ切⊙O于点A,∠BAQ=60°,连接BO并延长与⊙O交于点C,与OA的延长线交于点T,若TC=2,求TA的长.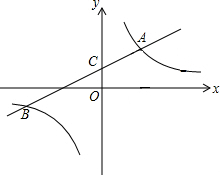 如图,一次函数y1=k1x+1与反比例函数y2=$\frac{k_2}{x}$的图象交于点A(3,2)和点B,与y轴交于点C.
如图,一次函数y1=k1x+1与反比例函数y2=$\frac{k_2}{x}$的图象交于点A(3,2)和点B,与y轴交于点C. 如图,l1∥l2,AB⊥l1,∠ABC=120°,则∠α=150°.
如图,l1∥l2,AB⊥l1,∠ABC=120°,则∠α=150°.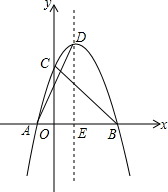 抛物线y=ax2+bx+3经过点A(-2,0),B(4,0),与y轴交于点C.
抛物线y=ax2+bx+3经过点A(-2,0),B(4,0),与y轴交于点C. 如图,已知AB=AE,∠1+∠2=∠3,∠ABC=∠AED=90°,求证:BC+DE=CD.
如图,已知AB=AE,∠1+∠2=∠3,∠ABC=∠AED=90°,求证:BC+DE=CD. 如图,已知AC⊥BD于点E,AB=BC,求证:∠1=∠2.
如图,已知AC⊥BD于点E,AB=BC,求证:∠1=∠2.