Question

3．如图，已知AB=AE，∠1+∠2=∠3，∠ABC=∠AED=90°，求证：BC+DE=CD．

Answer 1

分析 将△ABC旋转至△AEF，早∠1+∠2=∠3的条件，可得∠CAD=∠FAD，由SAS可证得△ACD与△AFD全等，从而CD=DF=DE+EF=DE+BC，得证．

解答 证明：∵AB=AE，∠ABC=∠AED=90°，
故将△ABC旋转至△AEF，如图，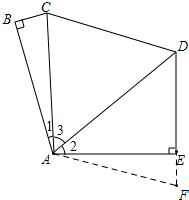

∴∠1=∠EAF，BC=EF，
∵∠1+∠2=∠3，
∴∠EAF+∠2=∠3，
即∠CAD=∠FAD，
在△CAD和△FAD中，
$\left\{\begin{array}{l}{CA=FA}\\{∠CAD=∠FAD}\\{AD=AD}\end{array}\right.$，
∴△ACD≌△AFD（SAS），
∴CD=FD=EF+DE=BC+DE．

点评 本题主要考查了全等三角形的判定与性质，难度中等．本题是一种基本的模型，即四边形有一组邻边相等且有一组对角互补时，可“旋转拼合”，这一技巧很常用，务必掌握．