Question

12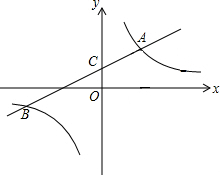．如图，一次函数y₁=k₁x+1与反比例函数y₂=$\frac{k_2}{x}$的图象交于点A（3，2）和点B，与y轴交于点C．
（1）分别求出这两个函数的表达式及点B的坐标；
（2）根据函数图象可知，当y₁＞y₂时，x的取值范围是-6＜x＜0或x＞3．

Answer 1

分析 （1）用待定系数法即可求出解析式，解方程组求出点B坐标．
（2）观察图象可以直接得到答案．

解答 解：（1）∵一次函数y₁=k₁x+1与反比例函数y₂=$\frac{k_2}{x}$的图象交于点A（3，2），
∴2=3k₁+1，k₁=$\frac{1}{3}$，k₂=6，
∴y₁=$\frac{1}{3}$x+1，y₂=$\frac{6}{x}$，
由$\left\{\begin{array}{l}{y=\frac{1}{3}x+1}\\{y=\frac{6}{x}}\end{array}\right.$得到$\left\{\begin{array}{l}{x=3}\\{y=2}\end{array}\right.或\left\{\begin{array}{l}{x=-6}\\{y=-1}\end{array}\right.$，
∴点B（-6，-1）．
（2）由图象可知y₁＞y₂时，-6＜x＜0或x＞3．
故答案为-6＜x＜0或x＞3．

点评 本题考查待定系数法求函数解析式、学会利用方程组求交点坐标，根据图象确定自变量的取值范围是解题的关键，也是函数图象这个章节的重要题型．