Question

6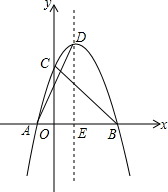．抛物线y=ax²+bx+3经过点A（-2，0），B（4，0），与y轴交于点C．
（1）求该抛物线的解析式：
（2）判断抛物线的顶点D与以BC为直径的⊙M的位置关系，并说明理由．
（3）点P在抛物线的对称轴上，点Q在x轴上，若四边形ACPQ为轴对称图形，求点P的坐标．

Answer 1

分析 （1）根据待定系数法，可得函数解析式；
（2）根据中点的性质，可得M点的坐标，根据勾股定理，可得BC，DM的长，根据点到圆心的距离与半径的关系，可得答案；
（3）根据等腰梯形，可得PC是上底，可得PC的坐标．

解答 解：（1）将A、B点坐标代入函数解析式，得
$\left\{\begin{array}{l}{4a-b+3=0}\\{16a+4b+3=0}\end{array}\right.$，
解得$\left\{\begin{array}{l}{a=-\frac{9}{24}}\\{b=\frac{3}{4}}\end{array}\right.$，
该抛物线的解析式为y=-$\frac{9}{24}$x²+$\frac{3}{4}$x+3；
（2）如图1，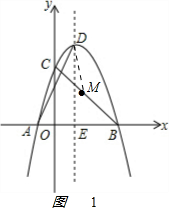
y=-$\frac{9}{24}$x²+$\frac{3}{4}$x+3的顶点坐标（1，$\frac{27}{8}$）．
当x=0时，y=3，即C（0，3），B（4，0），
M（2，$\frac{3}{2}$），BM=CM=$\frac{1}{2}$BC=$\frac{1}{2}$×$\sqrt{{3}^{2}+{4}^{2}}$=$\frac{5}{2}$．
DM=$\sqrt{（1-2）^{2}+（\frac{27}{8}-\frac{3}{2}）^{2}}$=$\frac{17}{8}$＞$\frac{5}{2}$，
抛物线的顶点D与以BC为直径的⊙M的外部；
（3）如图2，
等腰梯形ACPQ，PC∥AQ，P在对称轴上，得
P点的纵坐标为3，点的横坐标为1，
P点的坐标为（1，3）．

点评 本题考查了二次函数综合题，利用待定系数法求函数解析式；利用中点的性质得出M点的坐标是解题关键；利用等腰梯形得出PC是梯形的上底是解题关键．