题目内容
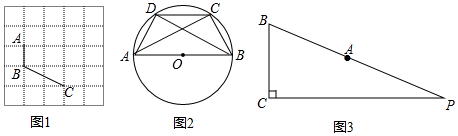
15.定义:数学活动课上,乐老师给出如下定义:有一组对边相等而另一组对边不相等的凸四边形叫做对等四边形.理解:(1)如图1,已知A、B、C在格点(小正方形的顶点)上,请在方格图中画出以格点为顶点,AB、BC为边的两个对等四边形ABCD;
(2)如图2,在圆内接四边形ABCD中,AB是⊙O的直径,AC=BD.求证:四边形ABCD是对等四边形;
(3)如图3,在Rt△PBC中,∠PCB=90°,BC=11,tan∠PBC=$\frac{12}{5}$,点A在BP边上,且AB=13.用圆规在PC上找到符合条件的点D,使四边形ABCD为对等四边形,并求出CD的长.
分析 (1)根据对等四边形的定义,进行画图即可;
(2)连接AC,BD,证明Rt△ADB≌Rt△ACB,得到AD=BC,又AB是⊙O的直径,所以AB≠CD,即可解答;
(3)根据对等四边形的定义,分两种情况:①若CD=AB,此时点D在D1的位置,CD1=AB=13;②若AD=BC=11,此时点D在D2、D3的位置,AD2=AD3=BC=11;利用勾股定理和矩形的性质,求出相关相关线段的长度,即可解答.
解答 解:(1)如图1所示(画2个即可).
(2)如图2,连接AC,BD,
∵AB是⊙O的直径,
∴∠ADB=∠ACB=90°,
在Rt△ADB和Rt△ACB中,
$\left\{\begin{array}{l}{AB=BA}\\{BD=AC}\end{array}\right.$
∴Rt△ADB≌Rt△ACB,
∴AD=BC,
又∵AB是⊙O的直径,
∴AB≠CD,
∴四边形ABCD是对等四边形.
(3)如图3,点D的位置如图所示:
①若CD=AB,此时点D在D1的位置,CD1=AB=13;
②若AD=BC=11,此时点D在D2、D3的位置,AD2=AD3=BC=11,
过点A分别作AE⊥BC,AF⊥PC,垂足为E,F,
设BE=x,
∵tan∠PBC=$\frac{12}{5}$,
∴AE=$\frac{12}{5}x$,
在Rt△ABE中,AE2+BE2=AB2,
即${x}^{2}+(\frac{12}{5}x)^{2}=1{3}^{2}$,
解得:x1=5,x2=-5(舍去),
∴BE=5,AE=12,
∴CE=BC-BE=6,
由四边形AECF为矩形,可得AF=CE=6,CF=AE=12,
在Rt△AFD2中,$F{D}_{2}=\sqrt{A{{D}_{2}}^{2}-A{F}^{2}}=\sqrt{1{1}^{2}-{6}^{2}}=\sqrt{85}$,
∴$C{D}_{2}=CF-F{D}_{2}=12-\sqrt{85}$,$C{D}_{3}=CF+F{D}_{2}=12+\sqrt{85}$,
综上所述,CD的长度为13、12-$\sqrt{85}$或12+$\sqrt{85}$.
点评 本题主要考查了四边形的综合题,解题的关键是理解并能运用“等对角四边形”这个概念.在(3)中注意分类讨论思想的应用、勾股定理的应用.

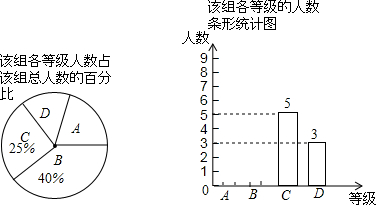
| 会员年卡类型 | 办卡费用(元) | 每次游泳收费(元) |
| A 类 | 50 | 25 |
| B 类 | 200 | 20 |
| C 类 | 400 | 15 |
| A. | 购买A类会员年卡 | B. | 购买B类会员年卡 | C. | 购买C类会员年卡 | D. | 不购买会员年卡 |
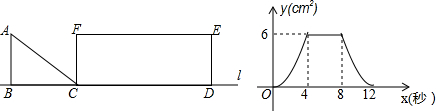
| A. | BC=4 | |
| B. | AB=3 | |
| C. | CD=10 | |
| D. | 当0≤x≤4时,y与x的函数关系式为y=$\frac{3}{8}$x2 |
 如图,在平面直角坐标系中,点A($\sqrt{3}$,1)、B(2,0)、O(0,0),反比例函数y=$\frac{k}{x}$图象经过点A.
如图,在平面直角坐标系中,点A($\sqrt{3}$,1)、B(2,0)、O(0,0),反比例函数y=$\frac{k}{x}$图象经过点A.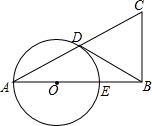 已知在△ABC中,∠B=90°,以AB上的一点O为圆心,以OA为半径的圆交AC于点D,交AB于点E.
已知在△ABC中,∠B=90°,以AB上的一点O为圆心,以OA为半径的圆交AC于点D,交AB于点E. 在?ABCD中,过点D作DE⊥AB于点E,点F 在边CD上,DF=BE,连接AF,BF.
在?ABCD中,过点D作DE⊥AB于点E,点F 在边CD上,DF=BE,连接AF,BF.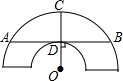 如图是一个古代车轮的碎片,小明为求其外圆半径,连接外圆上的两点A、B,并使AB与车轮内圆相切于点D,半径为OC⊥AB交外圆于点C.测得CD=10cm,AB=60cm,则这个车轮的外圆半径是50cm.
如图是一个古代车轮的碎片,小明为求其外圆半径,连接外圆上的两点A、B,并使AB与车轮内圆相切于点D,半径为OC⊥AB交外圆于点C.测得CD=10cm,AB=60cm,则这个车轮的外圆半径是50cm.