题目内容
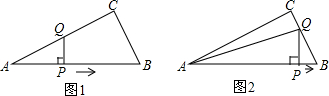
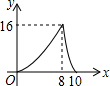
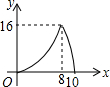
14.如图,Rt△ABC以1m/s的速度沿直线l匀速向矩形FCDE移动,直到点B与点D重合,AB=FC,设x秒时,三角形与矩形重叠部分的面积为ycm2,y与x的函数图象如图,则下列说法中错误的是( )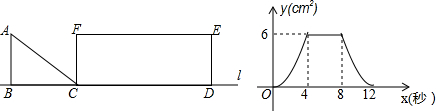
| A. | BC=4 | |
| B. | AB=3 | |
| C. | CD=10 | |
| D. | 当0≤x≤4时,y与x的函数关系式为y=$\frac{3}{8}$x2 |
分析 由题意和图象得出BC=4,BD=12,得出CD=8,得出A正确,C错误;
由B运动到C时,重叠部分的面积y=6,得出AB=4,得出B正确;
当0≤x≤4时,由MN∥AB,得出△MNC∽△ABC,得出比例式$\frac{MN}{AB}=\frac{NC}{BC}$,求出MN=$\frac{3}{4}x$,即可求出重叠部分的面积y与x的函数关系式,得出D正确.
解答 解:根据题意得:BC=4,BD=12,
∴CD=8,
∴A正确,C错误;
当B运动到C时,重叠部分的面积y=△ABC的面积=$\frac{1}{2}$BC•AB=6,
即$\frac{1}{2}$×4×AB=6,
∴AB=3,
∴B正确;
当0≤x≤4时,如图所示: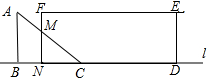 ∵MN∥AB,
∵MN∥AB,
∴△MNC∽△ABC,
∴$\frac{MN}{AB}=\frac{NC}{BC}$,
即$\frac{MN}{3}=\frac{x}{4}$,
∴MN=$\frac{3}{4}x$,
∴y=$\frac{1}{2}$NC•MN=$\frac{1}{2}$x•$\frac{3}{4}$x=$\frac{3}{8}$x2,
即y=$\frac{3}{8}$x2;
∴D正确;
故选:C.
点评 本题考查了动点问题的函数图象、相似三角形的判定与性质、三角形面积的计算;正确理解题意和图象,由图象得出相关信息是解决问题的关键.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
5.下列各式计算正确的是( )
| A. | $\sqrt{\frac{-4}{-9}}$=$\frac{\sqrt{-4}}{\sqrt{-9}}$=$\frac{-2}{-3}$=$\frac{2}{3}$ | B. | $\sqrt{4\frac{2}{9}}$=$\sqrt{\frac{38}{9}}$=2$\frac{1}{3}$$\sqrt{2}$ | ||
| C. | $\sqrt{\frac{3}{7}}$÷$\sqrt{3\frac{1}{2}}$=$\frac{\sqrt{6}}{7}$ | D. | $\sqrt{\frac{8}{25}}$=5$\sqrt{8}$ |
19. 如图,△ABC绕点A逆时针旋转40°后得到△ADF,且点D在BC边上,则∠B的度数为( )
如图,△ABC绕点A逆时针旋转40°后得到△ADF,且点D在BC边上,则∠B的度数为( )
 如图,△ABC绕点A逆时针旋转40°后得到△ADF,且点D在BC边上,则∠B的度数为( )
如图,△ABC绕点A逆时针旋转40°后得到△ADF,且点D在BC边上,则∠B的度数为( )| A. | 40° | B. | 50° | C. | 60° | D. | 70° |
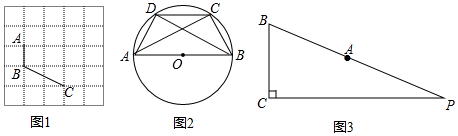
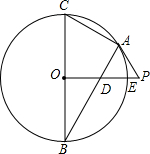 如图,已知PA与圆O相切于点A,直径BC⊥OP,线段OP与圆O交于点E,连接AB交PO于点D.
如图,已知PA与圆O相切于点A,直径BC⊥OP,线段OP与圆O交于点E,连接AB交PO于点D.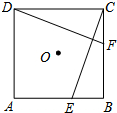 如图,E、F分别是正方形ABCD的边AB、BC上的点,BE=CF,连接CE、DF.△CDF可以看作是将△BCE绕正方形ABCD的中心O按逆时针方向旋转得到.则旋转的角度为90°.
如图,E、F分别是正方形ABCD的边AB、BC上的点,BE=CF,连接CE、DF.△CDF可以看作是将△BCE绕正方形ABCD的中心O按逆时针方向旋转得到.则旋转的角度为90°.