题目内容
7. 在?ABCD中,过点D作DE⊥AB于点E,点F 在边CD上,DF=BE,连接AF,BF.
在?ABCD中,过点D作DE⊥AB于点E,点F 在边CD上,DF=BE,连接AF,BF.(1)求证:四边形BFDE是矩形;
(2)若CF=3,BF=4,DF=5,求证:AF平分∠DAB.
分析 (1)根据平行四边形的性质,可得AB与CD的关系,根据平行四边形的判定,可得BFDE是平行四边形,再根据矩形的判定,可得答案;
(2)根据平行线的性质,可得∠DFA=∠FAB,根据等腰三角形的判定与性质,可得∠DAF=∠DFA,根据角平分线的判定,可得答案.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD.
∵BE∥DF,BE=DF,
∴四边形BFDE是平行四边形.
∵DE⊥AB,
∴∠DEB=90°,
∴四边形BFDE是矩形;
(2)解:∵四边形ABCD是平行四边形,
∴AB∥DC,
∴∠DFA=∠FAB.
在Rt△BCF中,由勾股定理,得
BC=$\sqrt{F{C}^{2}+F{B}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∴AD=BC=DF=5,
∴∠DAF=∠DFA,
∴∠DAF=∠FAB,
即AF平分∠DAB.
点评 本题考查了平行四边形的性质,利用了平行四边形的性质,矩形的判定,等腰三角形的判定与性质,利用等腰三角形的判定与性质得出∠DAF=∠DFA是解题关键.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
17.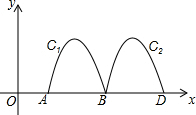 如图,抛物线y=-2x2+8x-6与x轴交于点A、B,把抛物线在x轴及其上方的部分记作C1,将C1向右平移得C2,C2与x轴交于点B,D.若直线y=x+m与C1、C2共有3个不同的交点,则m的取值范围是( )
如图,抛物线y=-2x2+8x-6与x轴交于点A、B,把抛物线在x轴及其上方的部分记作C1,将C1向右平移得C2,C2与x轴交于点B,D.若直线y=x+m与C1、C2共有3个不同的交点,则m的取值范围是( )
 如图,抛物线y=-2x2+8x-6与x轴交于点A、B,把抛物线在x轴及其上方的部分记作C1,将C1向右平移得C2,C2与x轴交于点B,D.若直线y=x+m与C1、C2共有3个不同的交点,则m的取值范围是( )
如图,抛物线y=-2x2+8x-6与x轴交于点A、B,把抛物线在x轴及其上方的部分记作C1,将C1向右平移得C2,C2与x轴交于点B,D.若直线y=x+m与C1、C2共有3个不同的交点,则m的取值范围是( )| A. | -2<m<$\frac{1}{8}$ | B. | -3<m<-$\frac{7}{4}$ | C. | -3<m<-2 | D. | -3<m<-$\frac{15}{8}$ |
18.把不等式x+2≤0的解集在数轴上表示出来,则正确的是( )
| A. |  | B. |  | C. |  | D. |  |
12. 学校抽查了30名学生参加“学雷锋社会实践”活动的次数,并根据数据绘制成了条形统计图,则30名学生参加活动的平均次数是( )
学校抽查了30名学生参加“学雷锋社会实践”活动的次数,并根据数据绘制成了条形统计图,则30名学生参加活动的平均次数是( )
 学校抽查了30名学生参加“学雷锋社会实践”活动的次数,并根据数据绘制成了条形统计图,则30名学生参加活动的平均次数是( )
学校抽查了30名学生参加“学雷锋社会实践”活动的次数,并根据数据绘制成了条形统计图,则30名学生参加活动的平均次数是( )| A. | 2 | B. | 2.8 | C. | 3 | D. | 3.3 |
19.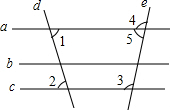 如图,下列说法错误的是( )
如图,下列说法错误的是( )
 如图,下列说法错误的是( )
如图,下列说法错误的是( )| A. | 若a∥b,b∥c,则a∥c | B. | 若∠1=∠2,则a∥c | ||
| C. | 若∠3=∠2,则b∥c | D. | 若∠3+∠5=180°,则a∥c |
5.下列各式计算正确的是( )
| A. | $\sqrt{\frac{-4}{-9}}$=$\frac{\sqrt{-4}}{\sqrt{-9}}$=$\frac{-2}{-3}$=$\frac{2}{3}$ | B. | $\sqrt{4\frac{2}{9}}$=$\sqrt{\frac{38}{9}}$=2$\frac{1}{3}$$\sqrt{2}$ | ||
| C. | $\sqrt{\frac{3}{7}}$÷$\sqrt{3\frac{1}{2}}$=$\frac{\sqrt{6}}{7}$ | D. | $\sqrt{\frac{8}{25}}$=5$\sqrt{8}$ |
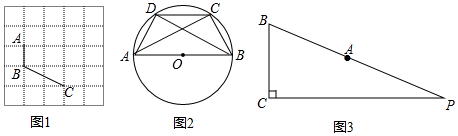
 如图是由射线AB,BC,CD,DE,EA组成的平面图形,则∠1+∠2+∠3+∠4+∠5=360°.
如图是由射线AB,BC,CD,DE,EA组成的平面图形,则∠1+∠2+∠3+∠4+∠5=360°.