题目内容
5.一种进价为每件40元的T恤,若销售单价为60元,则每周可卖出300件,为提高利益,就对该T恤进行涨价销售,经过调查发现,每涨价1元,每周要少卖出10件,请确定该T恤涨价后每周销售利润y(元)与销售单价x(元)之间的函数关系式,并求出销售单价定为多少元时,每周的销售利润最大?分析 用每件的利润乘以销售量即可得到每周销售利润,即y=(x-40)[300-10(x-60)],再把解析式整理为一般式,然后根据二次函数的性质确定销售单价定为多少元时,每周的销售利润最大.
解答 解:根据题意得y=(x-40)[300-10(x-60)]
=-10x2+1300x-36000,
∵x-60≥0且300-10(x-60)≥0,
∴60≤x≤90,
∵a=-10<0,
而抛物线的对称轴为直线x=65,即当x>65时,y随x的增大而减小,
而60≤x≤90,
∴当x=65时,y的值最大,
即销售单价定为65元时,每周的销售利润最大.
点评 本题考查了二次函数的应用:利用二次函数解决利润问题,在商品经营活动中,经常会遇到求最大利润,最大销量等问题.解此类题的关键是通过题意,确定出二次函数的解析式,然后确定其最大值,实际问题中自变量x的取值要使实际问题有意义,因此在求二次函数的最值时,一定要注意自变量x的取值范围.

练习册系列答案
相关题目
16.设二次函数y1=a(x-x1)(x-x2)(a≠0,x1≠x2)的图象与一次函数y2=dx+e(d≠0)的图象交于点(x1,0),若函数y=y1+y2的图象与x轴仅有一个交点,则( )
| A. | a(x1-x2)=d | B. | a(x2-x1)=d | C. | a(x1-x2)2=d | D. | a(x1+x2)2=d |
10.下列运算结果正确的是( )
| A. | x6÷x2=x3 | B. | (-x)-1=$\frac{1}{x}$ | C. | (2x3)2=4x6 | D. | -2a2•a3=-2a6 |
17.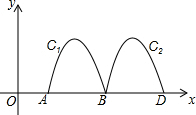 如图,抛物线y=-2x2+8x-6与x轴交于点A、B,把抛物线在x轴及其上方的部分记作C1,将C1向右平移得C2,C2与x轴交于点B,D.若直线y=x+m与C1、C2共有3个不同的交点,则m的取值范围是( )
如图,抛物线y=-2x2+8x-6与x轴交于点A、B,把抛物线在x轴及其上方的部分记作C1,将C1向右平移得C2,C2与x轴交于点B,D.若直线y=x+m与C1、C2共有3个不同的交点,则m的取值范围是( )
 如图,抛物线y=-2x2+8x-6与x轴交于点A、B,把抛物线在x轴及其上方的部分记作C1,将C1向右平移得C2,C2与x轴交于点B,D.若直线y=x+m与C1、C2共有3个不同的交点,则m的取值范围是( )
如图,抛物线y=-2x2+8x-6与x轴交于点A、B,把抛物线在x轴及其上方的部分记作C1,将C1向右平移得C2,C2与x轴交于点B,D.若直线y=x+m与C1、C2共有3个不同的交点,则m的取值范围是( )| A. | -2<m<$\frac{1}{8}$ | B. | -3<m<-$\frac{7}{4}$ | C. | -3<m<-2 | D. | -3<m<-$\frac{15}{8}$ |