题目内容
18．
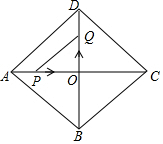如图，在菱形ABCD中，AD=5，AC=8，对角线AC，BD交于点O，P，Q分别是线段AO，DO上的动点，P从A出发以1cm/s的速度向O运动，Q从点O出发以2cm/s的速度向点D运动，设运动时间为t，四边形APQD面积为y．（1）求y与t的函数关系．
（2）当t为何值时，y有最值？并求其最值．
分析 （1）根据菱形的性质得AC⊥BD，OA=OC=$\frac{1}{2}$AC=4，则利用勾股定理可计算出OD=3，然后利用y=S△OAD-S△OPQ可表示出y=t2-4t+6（0≤t≤1.5）；
（2）利用二次函数的性质求解．
解答 解：（1）∵四边形ABCD为菱形，
∴AC⊥BD，OA=OC=$\frac{1}{2}$AC=3，
在Rt△AOD中，由勾股定理得OD=3，
AP=t，OQ=2t，则OP=4-t，
y=S△OAD-S△OPQ=$\frac{1}{2}$•3•4-$\frac{1}{2}$•（4-t）•2t=t2-4t+6（0≤t≤1.5）；
（2）y=（t-2）2+2，
当t=2时，y有最小值2，
当t=0时，y有最大值6．
点评 本题考查了菱形的性质：菱形具有平行四边形的一切性质；菱形的四条边都相等；菱形的两条对角线互相垂直，并且每一条对角线平分一组对角；菱形是轴对称图形，它有2条对称轴，分别是两条对角线所在直线．也考查了二次函数的性质．
练习册系列答案
相关题目
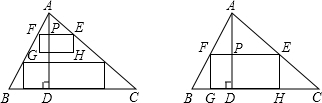如图，△ABC中，BC=10cm，BC边上的高AD=8cm，E、F分别为AC、AB上的点，且EF∥BC，以EF为边向下作矩形EFGH，且满足EF=2FG，设EF的长为x（cm），矩形EFGH与△ABC重叠部分的面积为y（cm2）．
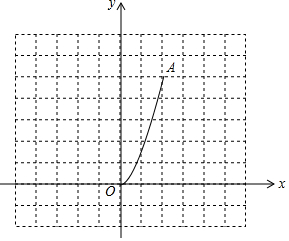如图，二次函数y=$\frac{5}{4}$x2（0≤x≤2）的图象记为曲线C1，将C1绕坐标原点O逆时针旋转90°，得曲线C2．
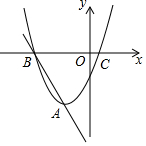已知抛物线y1=x2+2x-3的顶点为A，与x轴交于点B、C（B在C的左边），直线y2=kx+b过A、B两点．