题目内容
9.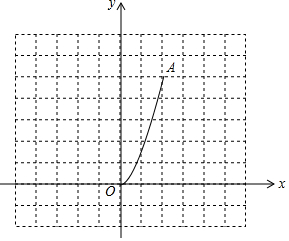 如图,二次函数y=$\frac{5}{4}$x2(0≤x≤2)的图象记为曲线C1,将C1绕坐标原点O逆时针旋转90°,得曲线C2.
如图,二次函数y=$\frac{5}{4}$x2(0≤x≤2)的图象记为曲线C1,将C1绕坐标原点O逆时针旋转90°,得曲线C2.(1)请画出C2;
(2)写出旋转后A(2,5)的对应点A1的坐标(-5,2);
(3)直接写出C1旋转至C2过程中扫过的面积$\frac{29}{4}$π.
分析 (1)根据图形旋转的性质画出曲线C2即可;
(2)根据点A1在坐标系中的位置即可得出结论;
(3)先求出OA的长,再由扇形的面积公式即可得出结论.
解答  解:(1)如图,曲线C2即为所求;
解:(1)如图,曲线C2即为所求;
(2)由图可知,A1(-5,2).
故答案为:(-5,2);
(3)∵OA=$\sqrt{{2}^{2}+{5}^{2}}$=$\sqrt{29}$,
∴C1旋转至C2过程中扫过的面积=$\frac{90π×29}{360}$=$\frac{29}{4}$π.
故答案为:$\frac{29}{4}$π.
点评 本题考查的是作图-旋转变换,熟知图形旋转不变性的性质是解答此题的关键.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
19.如今,优学派电子书包通过将信息技术与传统教学深度结合,让智能科技在现代教育中发挥了重要作用.某优学派公司筹集资金12.8万元,一次性购进两种新型电子书包访问智能终端:平板电脑和PC机共30台.根据市场需要,这些平板电脑、PC机可以全部销售,全部销售后利润不少于1.5万元,其中平板电脑、PC机的进价和售价见如下表格:
设该公司计划购进平板电脑x台,平板电脑和PC机全部销售后该公司获得的利润为y元.
(1)试写出y与x的函数关系式;
(2)该公司有哪几种进货方案可供选择?请写出具体方案;
(3)选择哪种进货方案,该公司获利最大?最大利润是多少元?
| 平板电脑 | PC机 | |
| 进价(元/台) | 5400 | 3500 |
| 售价(元/台) | 6100 | 3900 |
(1)试写出y与x的函数关系式;
(2)该公司有哪几种进货方案可供选择?请写出具体方案;
(3)选择哪种进货方案,该公司获利最大?最大利润是多少元?
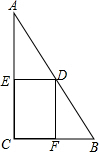 如图,在Rt△ABC中,已知∠C=90°,BC=4,AC=8,点D在斜边AB上,分别作DE⊥AC,DF⊥BC,垂足分别为E、F.得四边形DECF.设DE=x,DF=y
如图,在Rt△ABC中,已知∠C=90°,BC=4,AC=8,点D在斜边AB上,分别作DE⊥AC,DF⊥BC,垂足分别为E、F.得四边形DECF.设DE=x,DF=y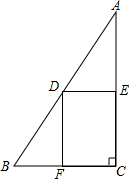 如图,在Rt△ABC中,∠C=90°,BC=6,AC=12,点D在斜边AB上,分别作DE⊥AC,DF⊥BC,垂足分别为点E,F,得四边形DECF,设DE=x,DF=y.
如图,在Rt△ABC中,∠C=90°,BC=6,AC=12,点D在斜边AB上,分别作DE⊥AC,DF⊥BC,垂足分别为点E,F,得四边形DECF,设DE=x,DF=y. 如图所示,D是BC的中点,E是AC的中点,若S△ADE=1,则S△ABC=4.
如图所示,D是BC的中点,E是AC的中点,若S△ADE=1,则S△ABC=4.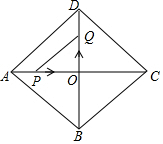 如图,在菱形ABCD中,AD=5,AC=8,对角线AC,BD交于点O,P,Q分别是线段AO,DO上的动点,P从A出发以1cm/s的速度向O运动,Q从点O出发以2cm/s的速度向点D运动,设运动时间为t,四边形APQD面积为y.
如图,在菱形ABCD中,AD=5,AC=8,对角线AC,BD交于点O,P,Q分别是线段AO,DO上的动点,P从A出发以1cm/s的速度向O运动,Q从点O出发以2cm/s的速度向点D运动,设运动时间为t,四边形APQD面积为y.