题目内容
5.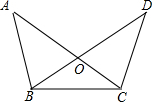 如图,在△OBC中,延长BO到D,延长CO到A,要证明OD=OA,则应添加条件中错误的是( )
如图,在△OBC中,延长BO到D,延长CO到A,要证明OD=OA,则应添加条件中错误的是( )| A. | △ABC≌△DCB | B. | OB=OC,∠A=∠D | C. | OB=OC,AB=DC | D. | ∠A=∠D,∠ABC=∠DCB |
分析 根据全等三角形的判定和性质,一一判断即可.
解答 解:A、正确.∵△ABC≌△DCB,
∴AC=BD,∠OCB=∠OBC,
∴OB=OC,
∴OA=OD,故选项正确.
B、正确.在△AOB和△DOC中,
$\left\{\begin{array}{l}{∠A=∠D}\\{∠AOB=∠DOC}\\{OB=OC}\end{array}\right.$,
∴△AOB≌△DOC,
∴AO=OD.故选项正确.
C、错误.SSA无法判断三角形全等,故选项错误.
D、正确.可以证明△ABC≌△DCB,由A可知正确.
故选C.
点评 本题考查全等三角形的判定和性质、等腰三角形的判定和性质等知识,解题的关键是正确寻找全等三角形解决问题,属于基础题,中考常考题型.

练习册系列答案
相关题目
16.下列方程中,有两个相等实数根的方程是( )
| A. | x(x-1)=0 | B. | x2-x+1=0 | C. | x2-2=0 | D. | x2-2x+1=0 |
13.若a是最大的负整数,b是绝对值最小的有理数,c是倒数等于它本身的自然数,则代表式a2015+2016b+c2017的值为( )
| A. | 2015 | B. | 2016 | C. | 2017 | D. | 0 |
20.九年级某班同学在毕业晚会中进行抽奖活动,在一个不透明的口袋中有三个完全相同的小球,把它们分别标号1、2、3,随机摸出一个小球记下标号后放回摇匀,再从中随机摸出一个小球记下标号,规定当两次摸出的小球标号相同时中奖,则中奖的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | 1 | D. | $\frac{4}{3}$ |
19.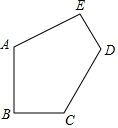 如图,已知AB=AE=$\sqrt{3}$,BC=DE=1,∠B=∠E=90°,∠A=120°,五边形ABCDE的面积是( )
如图,已知AB=AE=$\sqrt{3}$,BC=DE=1,∠B=∠E=90°,∠A=120°,五边形ABCDE的面积是( )
 如图,已知AB=AE=$\sqrt{3}$,BC=DE=1,∠B=∠E=90°,∠A=120°,五边形ABCDE的面积是( )
如图,已知AB=AE=$\sqrt{3}$,BC=DE=1,∠B=∠E=90°,∠A=120°,五边形ABCDE的面积是( )| A. | 4 | B. | 2$\sqrt{3}$ | C. | 8 | D. | 4$\sqrt{3}$ |
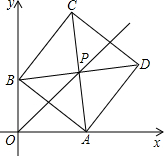 在平面直角坐标系xOy中,边长为2的正方形ABCD的对角线AC、BD相交于点P,顶点A在x轴正半轴上运动,顶点B在y轴正半轴上运动(x轴的正半轴、y轴的正半轴都不包含原点O),顶点C,D都在第一象限.
在平面直角坐标系xOy中,边长为2的正方形ABCD的对角线AC、BD相交于点P,顶点A在x轴正半轴上运动,顶点B在y轴正半轴上运动(x轴的正半轴、y轴的正半轴都不包含原点O),顶点C,D都在第一象限.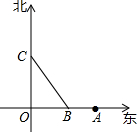 如图,甲船从点O出发,自南向北以40海里/时的速度行驶;乙船在点O正东方向120海里的A处,以30海里/时的速度自东向西行驶,经过2或$\frac{22}{25}$小时两船的距离为100海里.
如图,甲船从点O出发,自南向北以40海里/时的速度行驶;乙船在点O正东方向120海里的A处,以30海里/时的速度自东向西行驶,经过2或$\frac{22}{25}$小时两船的距离为100海里.