题目内容
19.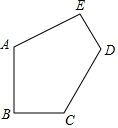 如图,已知AB=AE=$\sqrt{3}$,BC=DE=1,∠B=∠E=90°,∠A=120°,五边形ABCDE的面积是( )
如图,已知AB=AE=$\sqrt{3}$,BC=DE=1,∠B=∠E=90°,∠A=120°,五边形ABCDE的面积是( )| A. | 4 | B. | 2$\sqrt{3}$ | C. | 8 | D. | 4$\sqrt{3}$ |
分析 连接AC、AD,作AM⊥CD于M,由SSS证明△ABC′≌△AED,得出AC=AD,∠BAC=∠EAD,由勾股定理得出AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=2=2BC,求出∠EAD=∠BAC=30°,∠CAD=60°,证出△ACD是等边三角形,得出CD=AC=2,AM=$\sqrt{3}$,五边形ABCDE的面积=△ABC的面积+△AED的面积+△ACD的面积,即可得出结果.
解答 解: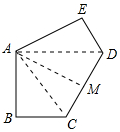 连接AC、AD,作AM⊥CD于M,如图所示:
连接AC、AD,作AM⊥CD于M,如图所示:
在△ABC和△AED中,$\left\{\begin{array}{l}{AB=AE}&{\;}\\{∠B=∠E}&{\;}\\{BC=ED}&{\;}\end{array}\right.$,
∴△ABC≌△AED(SAS),
∴AC=AD,∠BAC=∠EAD,
∵AB=$\sqrt{3}$,BC=1,∠ABC=90°,
∴AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=2=2BC,
∴∠EAD=∠BAC=30°,
∵∠BAE=120°,
∴∠CAD=60°,
∴△ACD是等边三角形,
∴CD=AC=2,CM=1,
∴AM=$\sqrt{3}$,
∴五边形ABCDE的面积=△ABC的面积+△AED的面积+△ACD的面积=2×$\frac{1}{2}$×1×$\sqrt{3}$+$\frac{1}{2}$×2×$\sqrt{3}$=2$\sqrt{3}$;
故选:B.
点评 本题考查了全等三角形的判定和性质、含30°角的直角三角形的性质、勾股定理、等边三角形的判定与性质以及三角形面积的计算;熟练掌握等边三角形的判定与性质,证明三角形全等是解决问题的关键.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案
相关题目
5.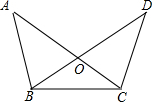 如图,在△OBC中,延长BO到D,延长CO到A,要证明OD=OA,则应添加条件中错误的是( )
如图,在△OBC中,延长BO到D,延长CO到A,要证明OD=OA,则应添加条件中错误的是( )
 如图,在△OBC中,延长BO到D,延长CO到A,要证明OD=OA,则应添加条件中错误的是( )
如图,在△OBC中,延长BO到D,延长CO到A,要证明OD=OA,则应添加条件中错误的是( )| A. | △ABC≌△DCB | B. | OB=OC,∠A=∠D | C. | OB=OC,AB=DC | D. | ∠A=∠D,∠ABC=∠DCB |
11.在下列方程中,有实数根的是( )
| A. | x2+3x+5=0 | B. | $\sqrt{2x+1}$+3=0 | C. | $\frac{x}{x-2}$=$\frac{2}{x-2}$ | D. | -x2+x+3=0 |
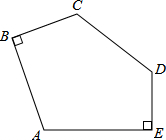 如图,已知AB=CD=AE=BC+DE=4,∠ABC=∠AED=90°,则五边形ABCDE的面积为16.
如图,已知AB=CD=AE=BC+DE=4,∠ABC=∠AED=90°,则五边形ABCDE的面积为16.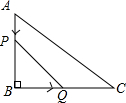 如图,在△ABC中,∠B=90°,AB=6cm,BC=12cm.动点P从A点开始沿AB向B点以1cm/s的速度运动(不与B点重合),动点Q从B点开始沿BC以2cm/s的速度向C点运动(不与C重合).如果P、Q同时出发,四边形APQC的面积最小时,要经过3秒.
如图,在△ABC中,∠B=90°,AB=6cm,BC=12cm.动点P从A点开始沿AB向B点以1cm/s的速度运动(不与B点重合),动点Q从B点开始沿BC以2cm/s的速度向C点运动(不与C重合).如果P、Q同时出发,四边形APQC的面积最小时,要经过3秒.