题目内容
16．下列方程中，有两个相等实数根的方程是（ ）| A． | x（x-1）=0 | B． | x2-x+1=0 | C． | x2-2=0 | D． | x2-2x+1=0 |
分析 根据根的判别式逐一判断即可．
解答 解：A、x（x-1）=0的两根为0或1，故此选项错误；
B、x2-x+1=0中△=1-4×1×1=-3＜0，无实数根，故此选项错误；
C、x2-2=0的两根为±$\sqrt{2}$，故此选项错误；
D、x2-2x+1=0中△=4-4×1×1=0，方程有两个相等的实数根，故此选项正确；
故选：D．
点评 本题主要考查根的判别式，熟练掌握根的情况与判别式间的关系是解题的关键．
练习册系列答案
课堂练加测系列答案
轻松课堂单元测试AB卷系列答案
相关题目
11．$\sqrt{2}$的倒数是（ ）
| A． | $\sqrt{2}$ | B． | $-\frac{\sqrt{2}}{2}$ | C． | $-\sqrt{2}$ | D． | $\frac{\sqrt{2}}{2}$ |
如图，点P是?ABCD边AB上的一点，射线CP交DA的延长线于点E，请从图中找出一对相似三角形：△EAP∽△EDC（答案不唯一）．
8．
如图，在坐标系中放置一菱形OABC，已知∠ABC=60°，点B在y轴上，OA=1，先将菱形OABC沿x轴的正方向无滑动翻转，每次翻转60°，连续翻转2017次，点B的落点依次为B1，B2，B3，…，则B2017的坐标为（ ）
如图，在坐标系中放置一菱形OABC，已知∠ABC=60°，点B在y轴上，OA=1，先将菱形OABC沿x轴的正方向无滑动翻转，每次翻转60°，连续翻转2017次，点B的落点依次为B1，B2，B3，…，则B2017的坐标为（ ）| A． | （1345，0） | B． | （1345.5，$\frac{\sqrt{3}}{2}$） | C． | （1345，$\frac{\sqrt{3}}{2}$） | D． | （1345.5，0） |
5．
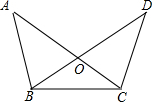如图，在△OBC中，延长BO到D，延长CO到A，要证明OD=OA，则应添加条件中错误的是（ ）
如图，在△OBC中，延长BO到D，延长CO到A，要证明OD=OA，则应添加条件中错误的是（ ）| A． | △ABC≌△DCB | B． | OB=OC，∠A=∠D | C． | OB=OC，AB=DC | D． | ∠A=∠D，∠ABC=∠DCB |
11．在下列方程中，有实数根的是（ ）
| A． | x2+3x+5=0 | B． | $\sqrt{2x+1}$+3=0 | C． | $\frac{x}{x-2}$=$\frac{2}{x-2}$ | D． | -x2+x+3=0 |