题目内容
10.已知x>y,若对任意实数a,以下结论:甲:ax>ay;乙:a2-x>a2-y;丙:a2+x≤a2+y;丁:a2x≥a2y
其中正确的是( )
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
分析 根据不等式的性质,可得答案.
解答 解:甲:ax>ay,a≤0,不成立;
乙:a2-x>a2-y两边都乘以-1,不等号的方向不改变,不成立;
丙:a2+x≤a2+y两边都加同一个整式,不等号的方向不变,不成立;
丁:a2x≥a2y两边都乘以非负数,不等号的方向不变,成立,
故选:D.
点评 本题考查了不等式的性质,不等式的基本性质:不等式两边加(或减)同一个数(或式子),不等号的方向不变;不等式两边乘(或除以)同一个正数,不等号的方向不变;不等式两边乘(或除以)同一个负数,不等号的方向改变.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
18.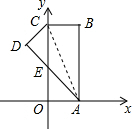 如图,在直角坐标系中,矩形OABC的边OA在x轴上,边OC在y轴上,点B的坐标为(1,3),将矩形沿对角线AC翻折,B点落在D点的位置,且AD交y轴于点E,那么点D的坐标为( )
如图,在直角坐标系中,矩形OABC的边OA在x轴上,边OC在y轴上,点B的坐标为(1,3),将矩形沿对角线AC翻折,B点落在D点的位置,且AD交y轴于点E,那么点D的坐标为( )
 如图,在直角坐标系中,矩形OABC的边OA在x轴上,边OC在y轴上,点B的坐标为(1,3),将矩形沿对角线AC翻折,B点落在D点的位置,且AD交y轴于点E,那么点D的坐标为( )
如图,在直角坐标系中,矩形OABC的边OA在x轴上,边OC在y轴上,点B的坐标为(1,3),将矩形沿对角线AC翻折,B点落在D点的位置,且AD交y轴于点E,那么点D的坐标为( )| A. | (-$\frac{1}{2}$,$\frac{13}{5}$) | B. | (-$\frac{2}{5}$,$\frac{13}{5}$) | C. | (-$\frac{4}{5}$,$\frac{12}{5}$) | D. | (-$\frac{3}{5}$,$\frac{12}{5}$) |
5.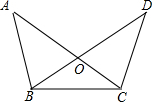 如图,在△OBC中,延长BO到D,延长CO到A,要证明OD=OA,则应添加条件中错误的是( )
如图,在△OBC中,延长BO到D,延长CO到A,要证明OD=OA,则应添加条件中错误的是( )
 如图,在△OBC中,延长BO到D,延长CO到A,要证明OD=OA,则应添加条件中错误的是( )
如图,在△OBC中,延长BO到D,延长CO到A,要证明OD=OA,则应添加条件中错误的是( )| A. | △ABC≌△DCB | B. | OB=OC,∠A=∠D | C. | OB=OC,AB=DC | D. | ∠A=∠D,∠ABC=∠DCB |
5.使式子$\frac{\sqrt{x-1}}{x-2}$有意义的x的范围是( )
| A. | x≥1 | B. | x≥1且x≠2 | C. | x≤1 | D. | x>2 |
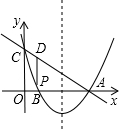 如图,抛物线y=x2+bx+c过点A(3,0),B(1,0),交y轴于点C,点P是该抛物线上一动点,点P从点C沿抛物线向A点运动(运动到A点停止),过点P作PD∥y轴交直线AC于点D.
如图,抛物线y=x2+bx+c过点A(3,0),B(1,0),交y轴于点C,点P是该抛物线上一动点,点P从点C沿抛物线向A点运动(运动到A点停止),过点P作PD∥y轴交直线AC于点D. 如图,点P是?ABCD边AB上的一点,射线CP交DA的延长线于点E,请从图中找出一对相似三角形:△EAP∽△EDC(答案不唯一).
如图,点P是?ABCD边AB上的一点,射线CP交DA的延长线于点E,请从图中找出一对相似三角形:△EAP∽△EDC(答案不唯一).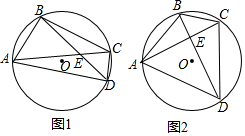 已知:⊙O是四边形ABCD的外接圆,AC与BD交于点E.
已知:⊙O是四边形ABCD的外接圆,AC与BD交于点E.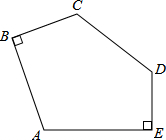 如图,已知AB=CD=AE=BC+DE=4,∠ABC=∠AED=90°,则五边形ABCDE的面积为16.
如图,已知AB=CD=AE=BC+DE=4,∠ABC=∠AED=90°,则五边形ABCDE的面积为16.