题目内容
20.解方程:$\frac{x+2}{x-2}-\frac{x}{x+2}=\frac{16}{{{x^2}-4}}$.分析 直接找出最简公分母,进而去分母求出答案.
解答 解:方程两边同乘以(x+2)(x-2)得:
(x+2)2-x(x-2)=16,
整理得:x=2,
检验:当x=2时,(x+2)(x-2)=0,
故此方程无解.
点评 此题主要考查了解分式方程,正确掌握解分式方程的步骤是解题关键.

练习册系列答案
相关题目
5.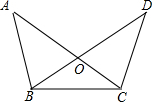 如图,在△OBC中,延长BO到D,延长CO到A,要证明OD=OA,则应添加条件中错误的是( )
如图,在△OBC中,延长BO到D,延长CO到A,要证明OD=OA,则应添加条件中错误的是( )
 如图,在△OBC中,延长BO到D,延长CO到A,要证明OD=OA,则应添加条件中错误的是( )
如图,在△OBC中,延长BO到D,延长CO到A,要证明OD=OA,则应添加条件中错误的是( )| A. | △ABC≌△DCB | B. | OB=OC,∠A=∠D | C. | OB=OC,AB=DC | D. | ∠A=∠D,∠ABC=∠DCB |
11.在下列方程中,有实数根的是( )
| A. | x2+3x+5=0 | B. | $\sqrt{2x+1}$+3=0 | C. | $\frac{x}{x-2}$=$\frac{2}{x-2}$ | D. | -x2+x+3=0 |
5.使式子$\frac{\sqrt{x-1}}{x-2}$有意义的x的范围是( )
| A. | x≥1 | B. | x≥1且x≠2 | C. | x≤1 | D. | x>2 |
12.若凸多边形的每个外角均为40°,过该多边形一个顶点的所有对角线条数是( )
| A. | 6 | B. | 8 | C. | 18 | D. | 27 |
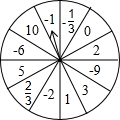 小亮自己设计了一个如图所示的自由转动的均匀的转盘,转盘被等分成12个扇形,每一个扇形里写有一个有理数,自由转动转盘,转盘停止后,分别求下列事件发生的概率:
小亮自己设计了一个如图所示的自由转动的均匀的转盘,转盘被等分成12个扇形,每一个扇形里写有一个有理数,自由转动转盘,转盘停止后,分别求下列事件发生的概率: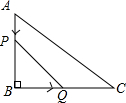 如图,在△ABC中,∠B=90°,AB=6cm,BC=12cm.动点P从A点开始沿AB向B点以1cm/s的速度运动(不与B点重合),动点Q从B点开始沿BC以2cm/s的速度向C点运动(不与C重合).如果P、Q同时出发,四边形APQC的面积最小时,要经过3秒.
如图,在△ABC中,∠B=90°,AB=6cm,BC=12cm.动点P从A点开始沿AB向B点以1cm/s的速度运动(不与B点重合),动点Q从B点开始沿BC以2cm/s的速度向C点运动(不与C重合).如果P、Q同时出发,四边形APQC的面积最小时,要经过3秒.