题目内容
4.在平面直角坐标系xOy中,点A的坐标是(0,-2),在x轴上任取一点M,连接AM,作线段AM的垂直平分线l1,过点M作x轴的垂线l2,记l1,l2的交点为P.在x轴上多次改变点M的位置,得到相应的点P,会发现这些点P竟然在一条抛物线L上!记点P(x,y),连接AP.(1)求出y关于x的函数解析式;
(2)若锐角∠APM的正切函数值为$\frac{4}{3}$.
①求点M的坐标;
②设点N在直线l2上,点Q在抛物线L上,当PN=1,且AQ,NQ之和最小时,求点Q的坐标.
分析 (1)利用垂直平分线的性质以及勾股定理得出y与x的函数关系式;
(2)①利用P点在第三、四象限分别得出M点坐标;
②根据题意首先得出N点坐标再利用待定系数法求出一次函数解析式,联立函数解析式进而得出Q点坐标.
解答 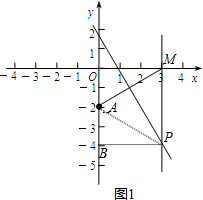 解:(1)如图1,连接AP,作PB⊥y轴于B,由l1垂直平分AM得:
解:(1)如图1,连接AP,作PB⊥y轴于B,由l1垂直平分AM得:
PA=PM=-y;
在Rt△ABP中,BP=OM=x,BA=PM-OA=-2-y,
根据勾股定理得:(-2-y)2+x2=y2,
整理得:y=-$\frac{1}{4}$x2-1.
(2)①当点P在第四象限时,设点P的坐标为(x,-$\frac{1}{4}$x2-1)(x>0).
∵直线l2垂直于x轴,
∴PM∥y轴.
∴∠APM=∠PAB,
∴tan∠PAB=tan∠PAB=$\frac{4}{3}$,即$\frac{BP}{AB}$=$\frac{4}{3}$.
∴$\frac{x}{-2+\frac{1}{4}x2+1}$=$\frac{4}{3}$,
解得x1=4,x2=-1(不合题意,舍去).
∴此时点M的坐标为(4,0).
当点P在第三象限时,由对称性同理可得点M的坐标为(-4,0).
综上可知,点M的坐标为(4,0)、(-4,0).
②如图2,当点M为(4,0)时,点P的坐标为(4,-5).
∵点N在直线l2上且PN=1,
∴点N的坐标为N1(4,-4)或N2(4,-6),
当点N在点P上方即N1(4,-4)时,连接AN1交抛物线于点Q1,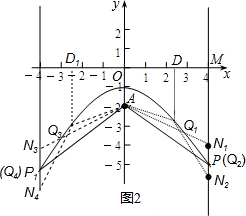
设直线AN1的解析式为y=kx+b(k≠0),把A(0,-2),N1(4,-4)代入得:
$\left\{\begin{array}{l}4k+b=-4\\ b=-2.\end{array}$
解得:$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=-2}\end{array}\right.$.
故直线AN1的解析式为:y=-$\frac{1}{2}$x-2.
由-$\frac{1}{2}$x-2=-$\frac{1}{4}$x2-1得,
解得:x1=1+$\sqrt{5}$,x2=1-$\sqrt{5}$(不合题意,舍去).
∴把x=1+$\sqrt{5}$代入y=-$\frac{1}{2}$x-2得点Q1的坐标为(1+$\sqrt{5}$,-$\frac{5+\sqrt{5}}{2}$).
当点N在点P下方即N2(4,-6)时,过点Q2作Q2D⊥x轴于D,
∵点Q2在此抛物线上,
∴Q2A=Q2D.
∴当AQ,NQ之和最小时即为NQ+QD最小,故此时点N2、Q2、D三点在一条直线上,此时点Q2与点P重合,即Q2(4,-5).
根据对称性,当点M为(-4,0)时,点P的坐标为(-4,-5).
∵点N在直线l2上且PN=1,
∴点N的坐标为N3(-4,-4)或N4(-4,-6),
当点N在点P1上方即N3(-4,-4)时,如图2,连接AN3交抛物线于点Q3,
设直线AN3的解析式为y=kx+b(k≠0),把A(0,-2),N3(-4,-4)代入得:
$\left\{\begin{array}{l}{-4k+b=-4}\\{b=-2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=\frac{1}{2}}\\{b=-2}\end{array}\right.$.
故直线AN3的解析式为:y=$\frac{1}{2}$x-2.
由$\frac{1}{2}$x-2=-$\frac{1}{4}$x2-1得,
解得:x1=-1+$\sqrt{5}$(不合题意,舍去),x2=-1-$\sqrt{5}$
∴把x=-1-$\sqrt{5}$代入y=$\frac{1}{2}$x-2得点Q3的坐标为(-1-$\sqrt{5}$,-$\frac{5+\sqrt{5}}{2}$).
当点N在点P下方即N4(4,-6)时,过点Q4作Q4D1⊥x轴于D1,
∵点Q2在此抛物线上,
∴Q4A=Q4D1.
∴当AQ,NQ之和最小时即为NQ+QD最小,故此时点N4、Q4、D1三点在一条直线上,此时点Q4与点P1重合,即Q4(-4,-5).
故点Q3(-1-$\sqrt{5}$,-$\frac{5+\sqrt{5}}{2}$),Q4(-4,-5),
综上所述:点Q的坐标为:Q1(1+$\sqrt{5}$,-$\frac{5+\sqrt{5}}{2}$),Q2(4,-5),Q3(-1-$\sqrt{5}$,-$\frac{5+\sqrt{5}}{2}$),Q4(-4,-5).
点评 此题主要考查了二次函数综合以及待定系数法求一次函数以及二次函数解析式以及函数交点求法等知识,利用P点位置不同得出M点坐标,注意不要漏解是解题关键.

 阅读快车系列答案
阅读快车系列答案 如图,AB∥CD,AC平分∠BCD,∠A=40°,则∠B的度数为( )
如图,AB∥CD,AC平分∠BCD,∠A=40°,则∠B的度数为( )| A. | 90° | B. | 100° | C. | 110° | D. | 120° |
| A. | 第一、二、三象限 | B. | 第一、二、四象限 | C. | 第二、三、四象限 | D. | 第一、三、四象限 |
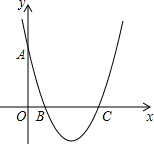 如图,对称轴为直线x=2的抛物线y=ax2+bx+c(a≠0)与x轴相交于B,C两点,其中B点坐标为(1,0),与y轴交于点A,A点坐标为(0,3)
如图,对称轴为直线x=2的抛物线y=ax2+bx+c(a≠0)与x轴相交于B,C两点,其中B点坐标为(1,0),与y轴交于点A,A点坐标为(0,3)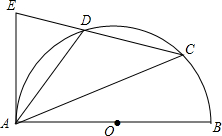 如图,AB是半圆⊙O的直径,点C是半圆上一个动点(不与点A,B重合),点D是弧AC的中点,延长CD交经过点A的切线于点E,连接AD,当△ADE是等腰三角形时,求∠BAC的度数.
如图,AB是半圆⊙O的直径,点C是半圆上一个动点(不与点A,B重合),点D是弧AC的中点,延长CD交经过点A的切线于点E,连接AD,当△ADE是等腰三角形时,求∠BAC的度数.