题目内容
5.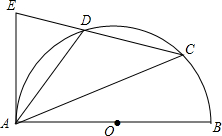 如图,AB是半圆⊙O的直径,点C是半圆上一个动点(不与点A,B重合),点D是弧AC的中点,延长CD交经过点A的切线于点E,连接AD,当△ADE是等腰三角形时,求∠BAC的度数.
如图,AB是半圆⊙O的直径,点C是半圆上一个动点(不与点A,B重合),点D是弧AC的中点,延长CD交经过点A的切线于点E,连接AD,当△ADE是等腰三角形时,求∠BAC的度数.
分析 连结BD,如图,利用圆周角定理得到∠B+∠BAD=90°,再根据切线的性质得∠2+∠BAD=90°,则∠B=∠2,再利用圆周角定理得到∠1=∠B=∠C,易得∠3=∠1+∠C=2=2∠2,根据等腰三角的性质讨论:当DE=DA时,则DE=DA=DC,此时点C与B点重合,不合题意舍去;当AD=AD,则∠E=∠3=2∠2,利用三角形内角和可计算∠2=36°,然后利用∠BAC=90°-∠1-∠2进行计算即可.
解答 解:连结BD,如图,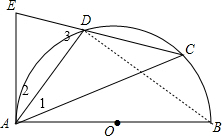 ∵AB是半圆⊙O的直径,
∵AB是半圆⊙O的直径,
∴∠ADB=90°,
∴∠B+∠BAD=90°,
∵AE为切线,
∴AB⊥AE,
∴∠BAE=90°,即∠2+∠BAD=90°,
∴∠B=∠2,
∵点D是弧AC的中点,
∴∠1=∠B=∠C,
∴∠1=∠2=∠C,
∴∠3=∠1+∠C=2=2∠2,
∵△ADE是等腰三角形,
当DE=DA时,则DE=DA=DC,此时点C与B点重合,不合题意舍去;
当AD=AD,则∠E=∠3=2∠2,
而∠E+∠3+∠2=180°,
∴2∠2+2∠2+∠2=180°,解得∠2=36°,
∴∠BAC=90°-∠1-∠2=90°-36°-36°=18°.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.解决本题的关键是证明∠1=∠2=∠C.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
13.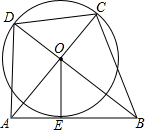 如图,Rt△AOB中,OA⊥OB,⊙O与AB相切于点E,AO、BD的延长线交⊙O于C、D.若⊙O的半径为1,则四边形ABCD面积最小值为( )
如图,Rt△AOB中,OA⊥OB,⊙O与AB相切于点E,AO、BD的延长线交⊙O于C、D.若⊙O的半径为1,则四边形ABCD面积最小值为( )
 如图,Rt△AOB中,OA⊥OB,⊙O与AB相切于点E,AO、BD的延长线交⊙O于C、D.若⊙O的半径为1,则四边形ABCD面积最小值为( )
如图,Rt△AOB中,OA⊥OB,⊙O与AB相切于点E,AO、BD的延长线交⊙O于C、D.若⊙O的半径为1,则四边形ABCD面积最小值为( )| A. | 2+3$\sqrt{2}$ | B. | $\frac{3+2\sqrt{2}}{2}$ | C. | 4+2$\sqrt{2}$ | D. | 3+3$\sqrt{2}$ |
20.成成在满分为100分的期中、期末数学测试中,两次的平均分为90分,若按期中数学成绩占30%,期末数学成绩占70%计算学期数学成绩,则成成的学期数学成绩可能是( )
| A. | 85 | B. | 88 | C. | 95 | D. | 100 |
14.下列运算正确的是( )
| A. | a2•a3=a6 | B. | ($\frac{1}{2}$)-1=-2 | C. | |-6|=6 | D. | $\sqrt{16}$=±4 |
15.下列运算正确的是( )
| A. | (-x2)4=x8 | B. | a6÷a2=a3 | C. | a2+a3=a5 | D. | (-a)${\;}^{-1}=\frac{1}{a}$ |
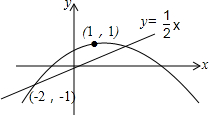 如图,二次函数y=ax2+bx+c的图象经过(-2,-1),(1,1)两点,下列判断:
如图,二次函数y=ax2+bx+c的图象经过(-2,-1),(1,1)两点,下列判断: