题目内容
19.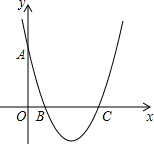 如图,对称轴为直线x=2的抛物线y=ax2+bx+c(a≠0)与x轴相交于B,C两点,其中B点坐标为(1,0),与y轴交于点A,A点坐标为(0,3)
如图,对称轴为直线x=2的抛物线y=ax2+bx+c(a≠0)与x轴相交于B,C两点,其中B点坐标为(1,0),与y轴交于点A,A点坐标为(0,3)(1)求此抛物线的解析式.
(2)求点B到直线AC的距离.
(3)在此抛物线的对称轴上,是否存在点P使得以点P,A,B为顶点的三角形是等腰三角形?若存在,求点P的坐标;若不存在,请说明理由.
分析 (1)直接利用对称轴以及B点坐标得出C点坐标,再利用交点式得出抛物线解析式;
(2)利用勾股定理得出AC的长,再利用三角形面积求法得出答案;
(3)分三种情况讨论:①当AP=AB时,②当AP=BP时,③当AB=BP时,分别求出答案.
解答 解:(1)由题意知,B,C关于对称轴x=2对称,B(1,0),
所以C(3,0),
设抛物线解析式为y=a(x-1)(x-3),
将A(0,3)代入得:
3a=3,
解得:a=1,
∴抛物线解析式为y=(x-1)(x-3)=x2-4x+3;
(2)如图1所示,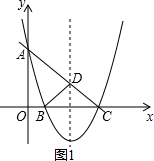
过B点作BD⊥AC交AC于D点
在Rt△AOC中,AC=$\sqrt{O{A}^{2}+O{C}^{2}}$=$\sqrt{9+9}$=3$\sqrt{2}$,
∴S△BCA=$\frac{1}{2}$BC•AD=$\frac{1}{2}$AC•BD,
=$\frac{1}{2}$×2×3,
=$\frac{1}{2}$AC•BD,
∴点B到直线AC的距离为$\sqrt{2}$;
(3)存在,抛物线的对称轴是直线x=2,P点在直线x=2上,设P的坐标(2,y)
∴AP2=22+(y-3)2=4+y2-6y+9=y2-6y+13,
BP2=(2-1)2+(y-0)2=1+y2,
AB2=12+32+1+9=10,
∵△PBA是等腰三角形,分三种情况讨论:
①如图2所示,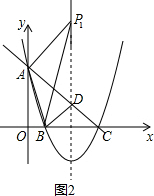
当AP=AB时,则AP2=AB2,
即y2-6y+13=10,
解得:y=3±$\sqrt{6}$,
∴P的坐标为(2,3+$\sqrt{6}$)或(2,3-$\sqrt{6}$);
②如图3,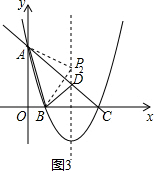
当AP=BP时,则AP2=BP2,即y2-6y+13=1+y2
解得:y=2,
∴P的坐标为(2,2)
③如图4,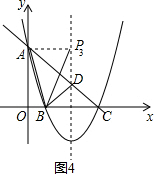
当AB=BP时,则AB2=BP2,即10=1+y2
解得:y=±3,
∴P的坐标为(2,3)或(2,-3),
当P的坐标为(2,-3)时,A,B,P在同一直线上,不符合题意,舍去.
∴综上所述,符合题意的点P有4个:P1(2,3+$\sqrt{6}$),P2(2,3-$\sqrt{6}$),P3(2,2),P4(2,3)
点评 此题主要考查了二次函数综合以及勾股定理、交点式、三角形面积求法等知识,正确分类讨论得出P点坐标是解题关键.

 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案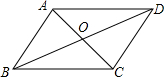 如图,四边形ABCD的对角线AC和BD交于点O,则下列不能判断四边形ABCD是平行四边形的条件是( )
如图,四边形ABCD的对角线AC和BD交于点O,则下列不能判断四边形ABCD是平行四边形的条件是( )| A. | OA=OC,AD∥BC | B. | ∠ABC=∠ADC,AD∥BC | ||
| C. | AB=DC,AD=BC | D. | ∠ABD=∠ADB,∠BAO=∠DCO |
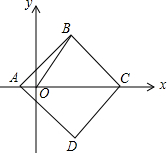 如图,在平面直角坐标系中,O为坐标原点,正方形ABCD的对角线AC落在x轴上,A(-1,0),C(7,0),连接OB,则∠BOC的正弦值为( )
如图,在平面直角坐标系中,O为坐标原点,正方形ABCD的对角线AC落在x轴上,A(-1,0),C(7,0),连接OB,则∠BOC的正弦值为( )| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
 如图,l1∥l2,∠3=30°,∠2=100°,则∠1=( )
如图,l1∥l2,∠3=30°,∠2=100°,则∠1=( )| A. | 100° | B. | 110° | C. | 120° | D. | 130° |
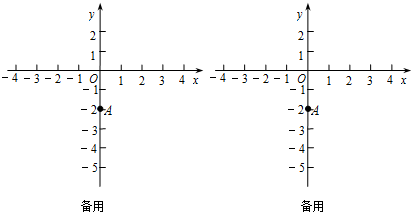
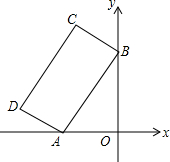 如图,矩形ABCD的两个顶点A,B在坐标轴上,AD:AB=1:2,且A(-2,0),∠BAO=60°,反比例函数y=$\frac{k}{x}$(k≠0)的图象恰好经过该矩形的顶点,则k=-2-$\sqrt{3}$或-6-$\sqrt{3}$.
如图,矩形ABCD的两个顶点A,B在坐标轴上,AD:AB=1:2,且A(-2,0),∠BAO=60°,反比例函数y=$\frac{k}{x}$(k≠0)的图象恰好经过该矩形的顶点,则k=-2-$\sqrt{3}$或-6-$\sqrt{3}$.